中学生では 1 次関数 や原点を通る 2 次関数のグラフを、高校生では 2 次関数を中心に、4 次関数くらいまでの関数のグラフが数学で登場します。 なかでも 2 次関数については詳しく学習するので、2 次関数「y = ;ax²bxc」の「aが正だったら下に凸(下に出っ張っている二次関数 ・2次関数の平方完成New! ・2次関数の平方完成からグラフへ ・2次関数のグラフ ・2次関数のグラフと係数の符号 ・2次関数の最大最小 ・2次関数の決定 ・2次関数平行対称移動 ・2次不等式の解法 ・2次不等式の解法2 ・2次不等式の解法32次関数の定義 2次関数のグラフ y =x2 y = x 2 のグラフ , y =ax2 y = a x 2 のグラフ , y =a(x−p)2q y = a ( x − p) 2 q のグラフ , y= ax2bxc y = a x 2 b x c のグラフ ASCIIsvgによるグラフの描画 , 2次関数のグラフ(拡大,平行移動) 2次関数の平方完成の仕方 2次
U9j580gf8iba369ji2w Xyz P 794
次関数
次関数-結果は次の通り。SUBSTITUTE関数を入力したセルに、「エクセル」を「Excel」に置き換えた文字列が表示されていますね。 1 2 3 次のページへ 更新日:17年07月07日 あわせて読みたい Windows 10パソコンのスクリーンショットを撮る5つの方法! PC画面を画像で保存するやり方 のし・熨斗紙のLINEST 関数の書式には、次の引数があります。 構文 既知の y 必ず指定します。 既にわかっている y の値の系列であり、y = mx b という関係が成り立ちます。 "既知の y" の配列が 1 つの列に入力されている場合、"既知の x" の各列はそれぞれ異なる変数であると見なされます。 "既知の y" の配列が
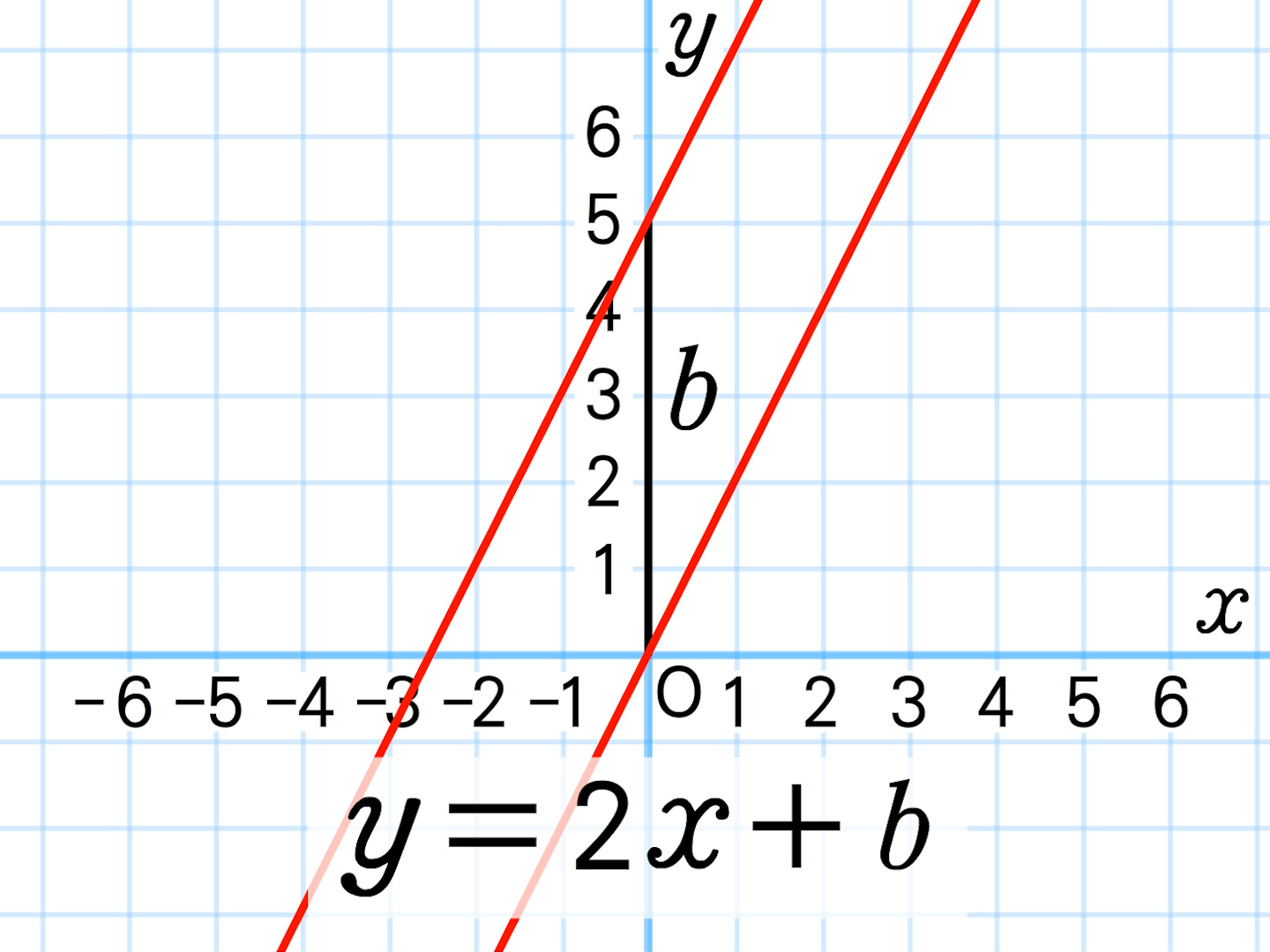



2年 1次関数のグラフ 1 数学イメージ動画集 大日本図書
Besselj 関数の書式には、次の引数があります。 x 必ず指定します。 関数に代入する値を指定します。 n 必ず指定します。 ベッセル関数の次数を指定します。 n に整数以外の値を指定すると、小数点以下が切り捨てられます。 解説 x に数値以外の値を指定すると、エラー値 #value!6 伝達関数1次の場合 これまで,伝達関数には,変数として j を使ってきましたが, これからは,これを s で表します. 今回は扱いませんが,この s はラプラス変数で, ラプラス変換を使えば過渡応答を求めることもできます. 正弦波に対する定常的な応答を求めるには,s に j を代入して二次関数の頂点と軸の求め方は別記事で解説しています。 ⇒二次関数の頂点・軸を平方完成で求める手順 \(y=2x^{2}4x\)の最大値・最小値 関数の式を変形すると \begin{eqnarray} y&=&2x^{2}4x\\ &=&2(x1)^{2}2 \end{eqnarray} この関数はグラフにすると下図のようになり
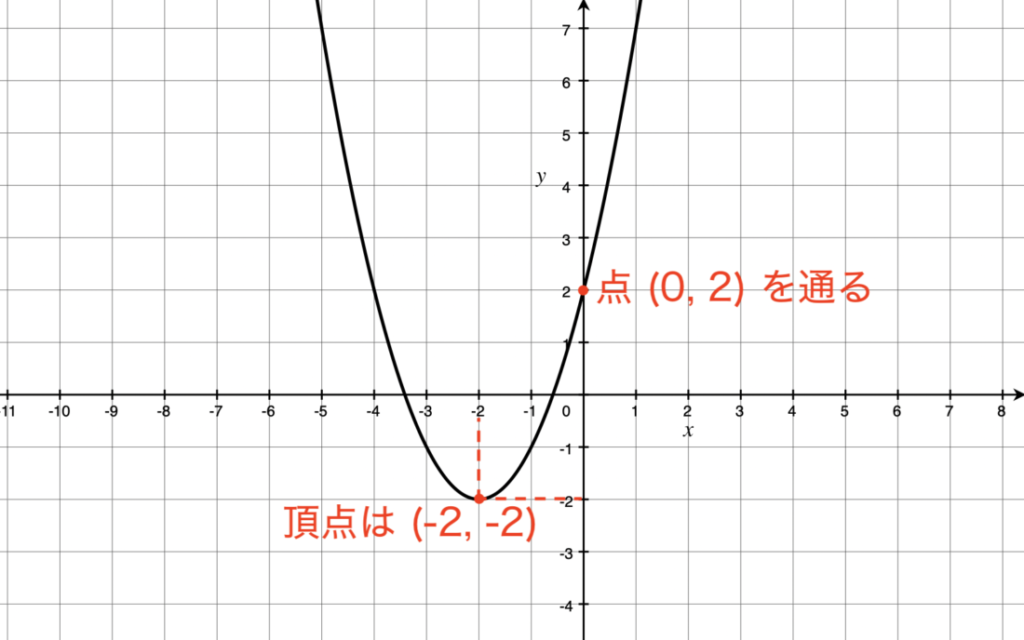
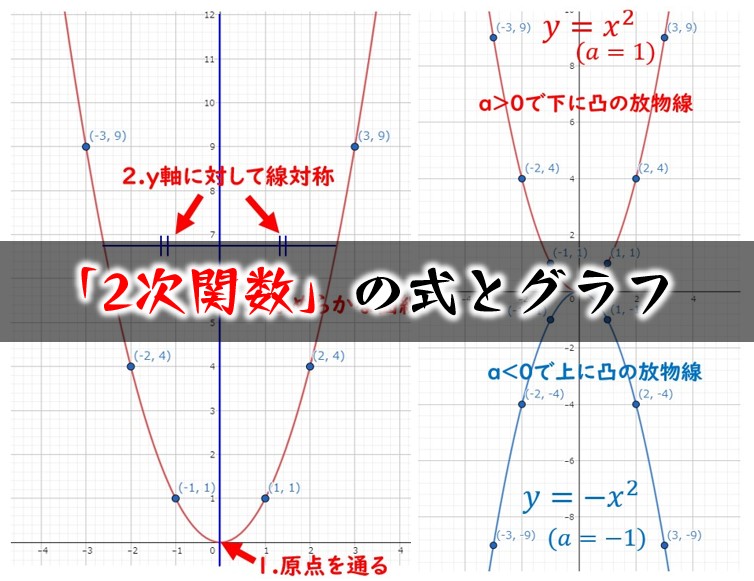
二次関数にじかんすう 2次の多項式で表される関数。 1変数の場合の一般形はf( x )=ax 2 +bx+c(a≠0)で,グラフはy軸に平行な軸をもつ放物線。 n変数の二次関数は(式1)の形に表される。 → 二次曲線 →関連項目 二次曲面 出典 株式会社平凡社 ①1次関数と反比例,②2次関数,③動点p ①,1次関数,反比例グラフ ・最初の等積変形(★★☆☆☆)(オリジナル) 実は等積変形でなくても解けるのですが,まあ練習用に。 ・順序だてて(★★☆☆☆)(オリジナル) 関数記述対策の初めの方に。 Processing 2次関数のグラフを書く(後編) 今日は,先日書いた2次関数のグラフをインタラクティブにします。 機能拡張する点は以下の通りとなります。 これでひと通りの2次関数のグラフは書けて,表示できるようになるはずです。 画面例を示します
2次方程式の解の存在範囲は, 「2次関数のグラフが x 軸と交わる部分」に関する問題に置き換えて考えることができます。 のがポイントですね。 グラフを利用して与えられた範囲内に, x 軸との共有点が存在する条件を, 視覚的に考えていきます。 今回の※この番組は、21年度の新作です。 10 6/14 1次方程式・1次不等式の応用 11 6/21 2次関数 関数 12 6/28 2 次関数の頂点 13 7/5 2 次関数のグラフをかく 14 7 次のコード例を使用して、実行の違いを確認することもできます。 待機(ms) 待機(ms)関数は、待機するミリ秒で指定された時間が経過するまで実行をブロックします。 例1 実行に5ミリ秒かかるコードを持つループを考えてみましょう。




2次方程式と2次関数の関係 数学i フリー教材開発コミュニティ Ftext



3次関数はどうなる 中学から数学だいすき
ところ,「1次関数」という意見があったので, 全体で座標軸の取り方を確認し,課題を設定 した。 (2) 課題追究について 課題追究に入ったとき,何から取り掛かれ ばよいのか戸惑う生徒も見られた。このよう な生徒にはヒントカードを配布し,課題解決 の過程を把握できるようにした。 (3二次関数の y=ax^2bxc というグラフを作成してみたいと思います。 定数の a と b と cを変更することができるように、下図のようなデータリストを作成しました。 定数 a の値を1,2,3,4と変えた場合のグラフを作成します。 定数 b と c の値は 0 としました。 xの値は ここでは ~ までの値とし 二変数の二次関数 f ( x, y) = a x 2 b x y c y 2 d x e y f f (x, y)=ax^2bxycy^2dxeyf f (x,y) = ax2 bxy cy2 dx eyf に関する問題は入試や定期試験で頻出なので,解き方を3つ紹介します。 目次 二変数の二次関数に関する問題 1:平方完成による解法 2:偏微分を




2次関数 膨大なページ数 Wiki




2次関数の書き方3パターン 数学の偏差値を上げて合格を目指す
Fxx(x, y) , fxy(x, y) , fyx(x, y) , fyy(x, y) これらを f(x, y) の 2次偏導関数 (または 2階偏導関数 )といいます。 当然,2次偏導関数が更に偏微分可能であれば,3次偏導関数を考えることができ,2次以上の偏導関数をまとめて 高次偏導関数 といいます。 本講座では1次関数をもう一度 ここでの内容は2次関数のときにも使えるものばかりです.しっかり理解しましょう. 1(そもそも)関数とは? 定義 定まった値をとる文字を定数,様々な値をとる文字を変数という. 変数の値のとりうる範囲を変域という. 注意円錐, 二次曲線, 楕円, 双曲線, 放物線, 二次関数 中学校で出てくる二次曲線(反比例と放物線)について調べてみると、面白いことがたくさんでてきます。 さらに広がってくる世界を覗いてみましょう。



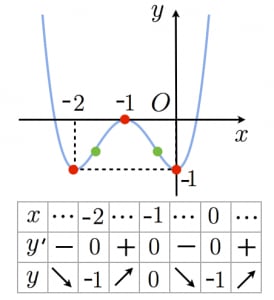
N次関数のグラフの概形 関谷 翔 Note




1次関数 1次関数の式の求め方 中学数学 定期テスト対策サイト
二次関数とそのグラフについて理解し,二次関数を用 いて数量の関係や変化を表現することの有用性を認識す るとともに,それらを事象の考察に活用できるようにす る。 ア 二次関数とそのグラフ 事象から二次関数で表される関係を見いだすこと。まが、二次関数の分野ではそれが見つけにくく親しみが持ちにくいと考える。しかし、日常をよく見てみればデジ タルカメラのズームや視力検査などたくさん二次関数y= が存在するのである。このことから、二次関数の 導入を生徒に抵抗なく理解させるにはどのようにすればよいかを考えたい1次関数とグラフのポイントは!・1次関数とは、 y と x が y = a x b の式で表される関係のこと。・x の係数 a を「傾き」 b を「切片」という!




高校数学 Y Ax 2のグラフ 下に凸 上に凸 映像授業のtry It トライイット



数学 二次関数グラフの書き方を初めから解説 Youtube
・2 次関数の最大・最小(文字定数をふくむ) について学習しました。学習内容をまとめておきますので,問題を解く前に確認しておきま しょう。 2 次関数の最大・最小 1 2 次関数の最大・最小 関数の値域に最大の値があるとき,その値を関数の最大値といい,最小の値があると き,その値を二次関数 最大最小 グラフが動く① のコピー ワークシート 大橋一生 Parabolas and straight lines(放物線と直線) ワークシート okyota Free Throw ワークシート Takaaki Masui 関数y=ax^2導入 ワークシート Geo_Math_Room 二次関数変域と領域 ワークシート Lamuda 軸が動く2次関数の最大・最小値 ワークシートブリタニカ国際大百科事典 小項目事典 1次関数の用語解説 関数のうち最も簡単であり,また応用範囲の広いもので,変数 x の2項1次式で表わされる関数である。これは一般に,f(x)=ax+b ( a≠0 ) の形で表わされ,a ,b は与えられた定数である。この関数は,線形関数とも呼ばれ,グラフは




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




中2 数学 1次関数1 Y Ax B 9分 Youtube



2次関数とは 1分でわかる意味 公式と計算 グラフ 平行移動との関係




中学数学 1次関数 2次関数 53 千葉県 東京都 高校入試問題 英語 数学 さくら教育研究所 中学 高校受験 Skredu



二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局




2次関数y A X 2 と直線y Mx Nとの交点 中学3年生の数学 身勝手な主張




2次関数のグラフ



中2 1次関数4




数学 中3 35 二次関数のグラフ Youtube



2年 1次関数と図形 数学イメージ動画集 大日本図書



3




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ




1次関数 2次関数で作るアート作品 Ex Gram エクスグラム 小中高生向けプログラミング教室



中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾




高校数学 関数は グラフが命 映像授業のtry It トライイット




3次関数のブロック分割 4等分割 おいしい数学
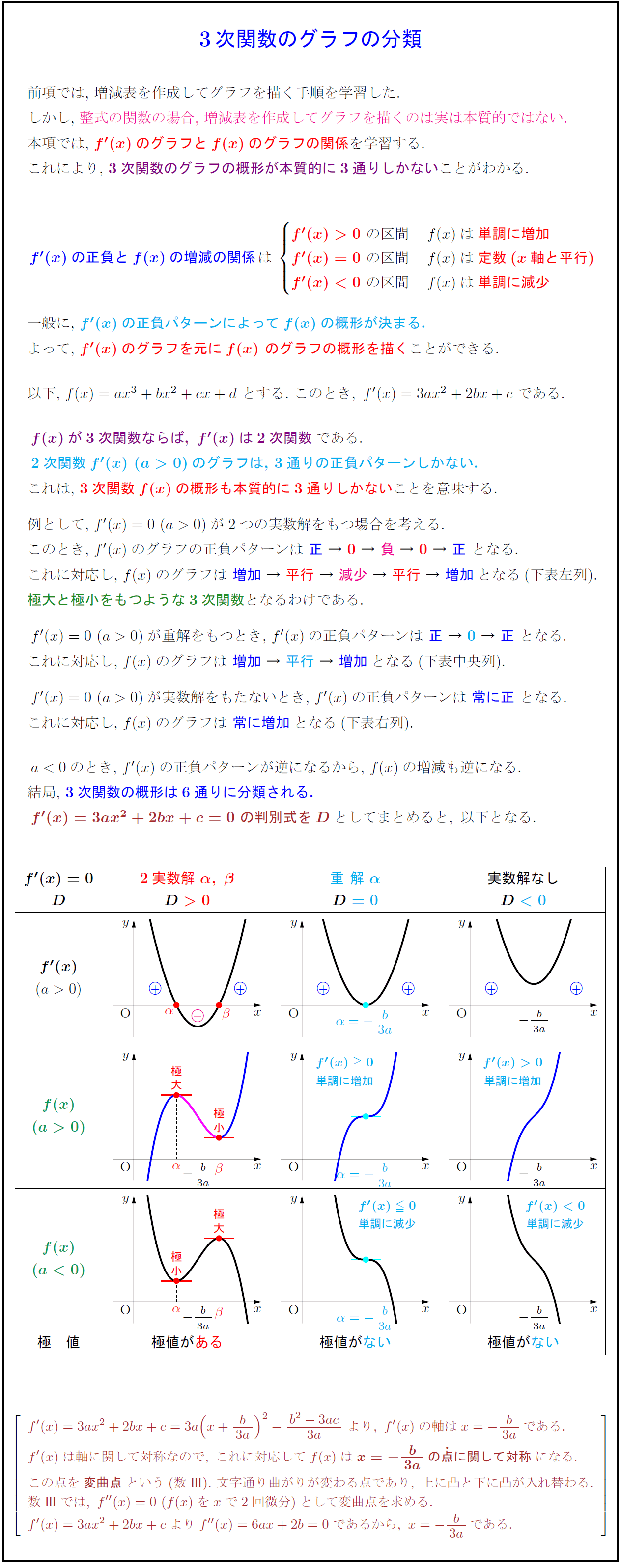



高校数学 3次関数のグラフの分類 F X のグラフとf X のグラフの関係 受験の月




3次関数の分類と点対称性 おいしい数学



四次関数のグラフの概形と例題2問 高校数学の美しい物語
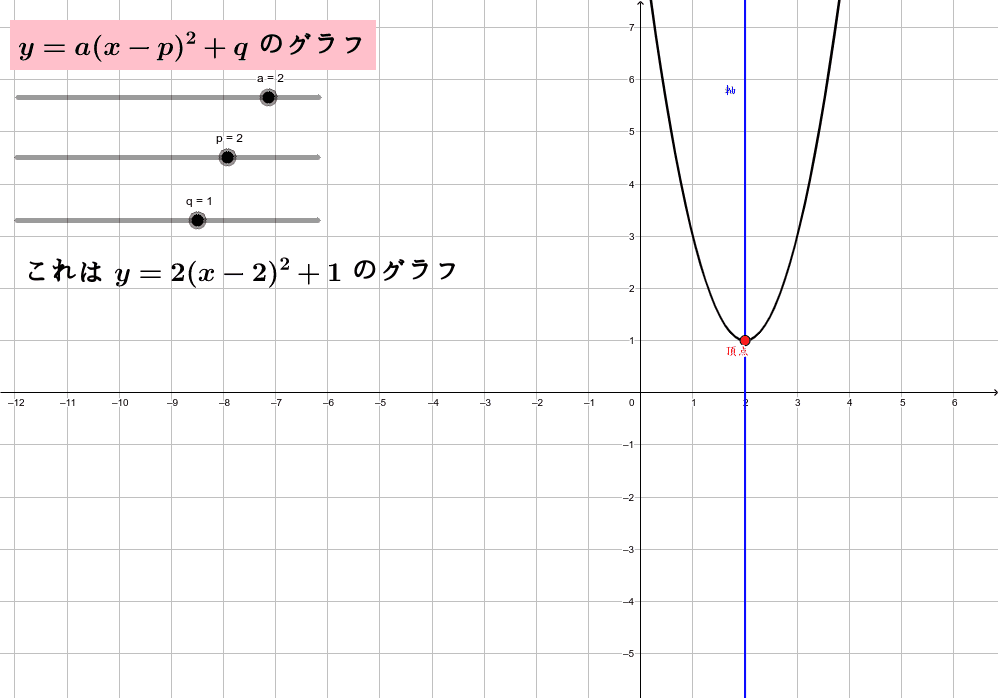



2次関数のグラフ Geogebra




二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局



3次関数の微積分 京極一樹の数学塾




2次関数 2次関数の決定について 日々是鍛錬 ひびこれたんれん



3




T 2次関数 とおいて4次関数の最大最小を求める方法 数学の偏差値を上げて合格を目指す



U9j580gf8iba369ji2w Xyz P 794



2次関数問題 Of 京極一樹の数学塾会員頁




数学1 2次関数勉強法 センター数学頻出の2次関数をマスターするポイント




必読 3次関数のグラフは解の個数と位置が大切 塾講師ステーション情報局



3次関数のグラフの等間隔性 大学入試数学の考え方と解法



1次関数 性質 中学から数学だいすき




数学1 基礎 2次関数 演習コース 数学1 基礎 演習コース 石井大裕 数学 Kindleストア Amazon
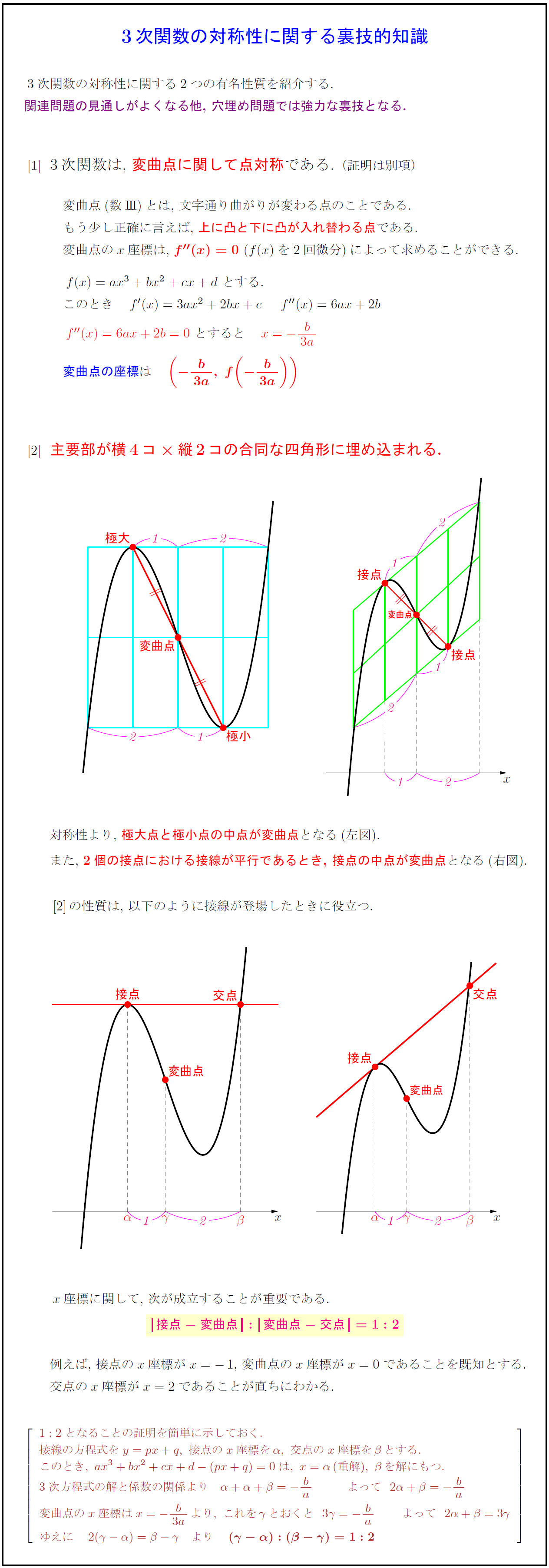



高校数学 3次関数の対称性に関する裏技的知識 受験の月



3次関数 面積を求める12分の1公式の証明とその使い方 Part2 大学入試数学の考え方と解法




二次関数 Wikipedia
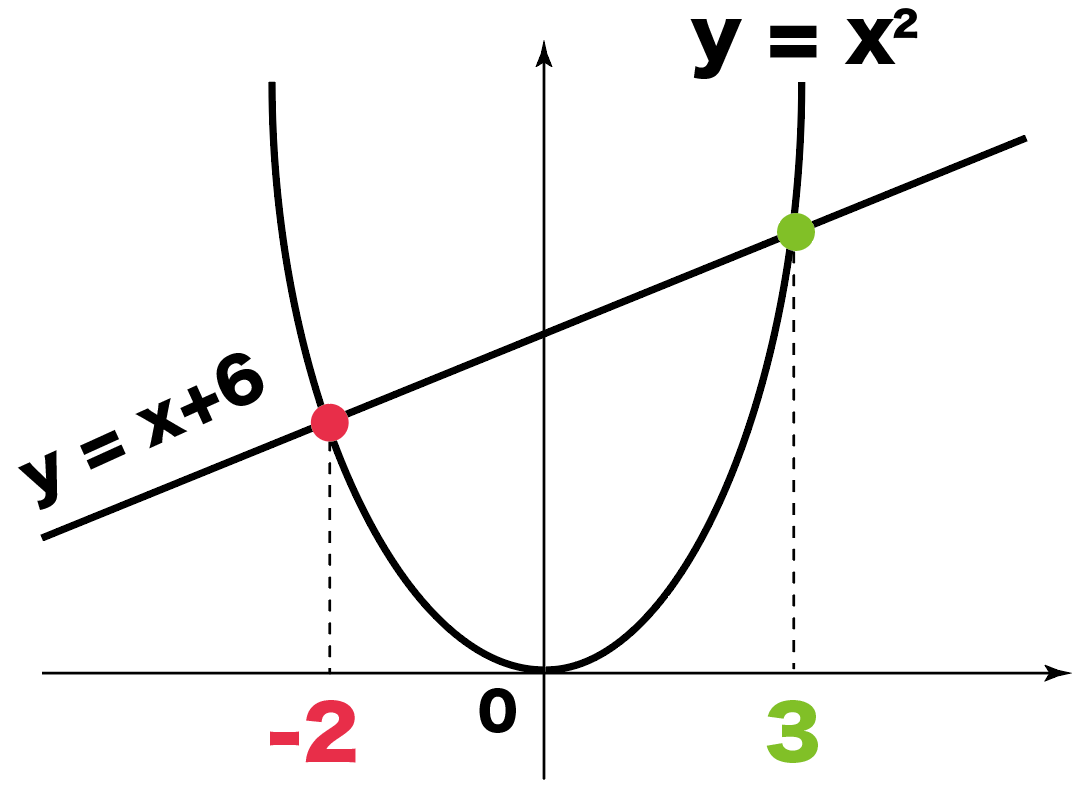



一次関数と二次関数の交点の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




1次関数の表から変化の割合 Geogebra
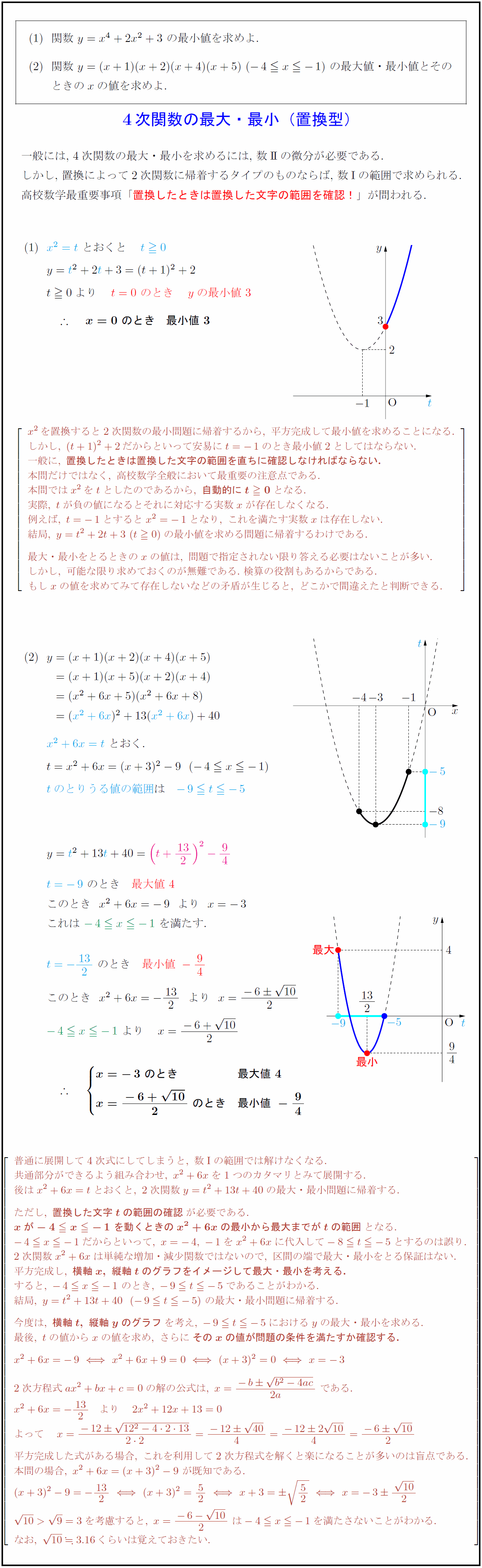



高校数学 4次関数の最大 最小 置換型 受験の月




4次関数の最大最小を 平方完成 を応用して解いてみよう 複2次式とは 遊ぶ数学




3次関数のブロック分割 4等分割 おいしい数学



1




二次関数の場合分けで 最小値を2つに分ける時と3つに分ける時の違いはなんですか Clear



Q Tbn And9gcrgpzd6zrnsfvmnyzeksxevrtufuxjv2q6waxpw9rngtt04aulp Usqp Cau



中学2年生数学 1次関数 グラフと図形 長野地区 Itto個別指導学院 長野市の学習塾
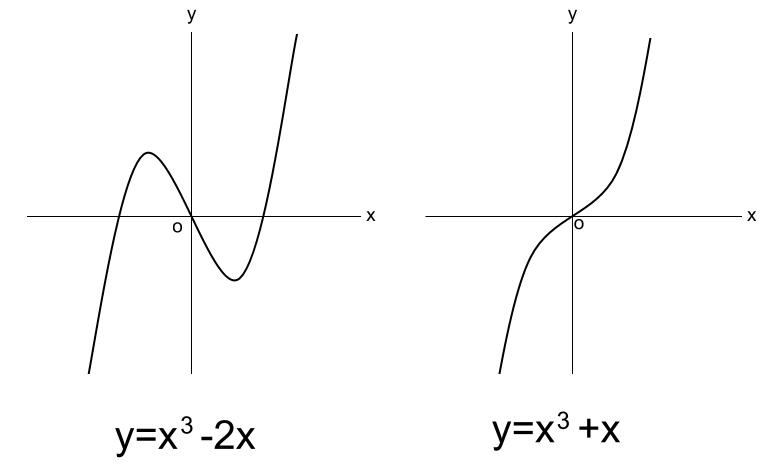



3次関数のグラフ 高校数学の無料オンライン学習サイトko Su




中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく
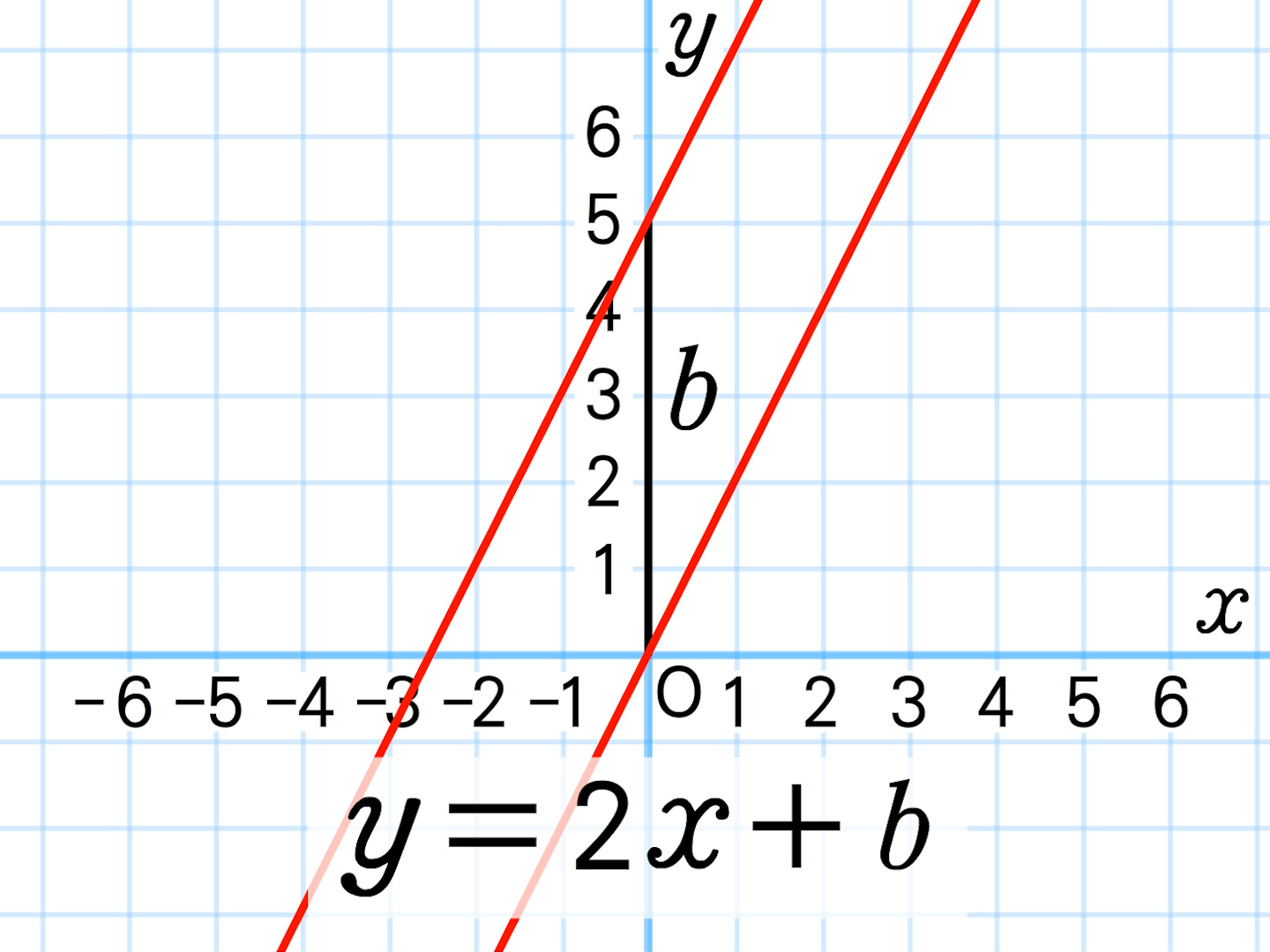



2年 1次関数のグラフ 1 数学イメージ動画集 大日本図書




5次関数のグラフ 大阪医科大学18年前期数学第1問 理系のための備忘録



二次関数とは 平方完成の公式や最大値 最小値 決定の問題 受験辞典



2次関数と1次関数の合成



2次関数とは 式とグラフの解説 数学fun



数学i Aチェック リピート 第2章 2最大 最小 2 2次関数の最大 最小 Pukiwiki
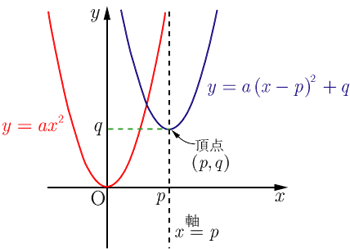



2次関数のグラフ Y A X 2 P Q
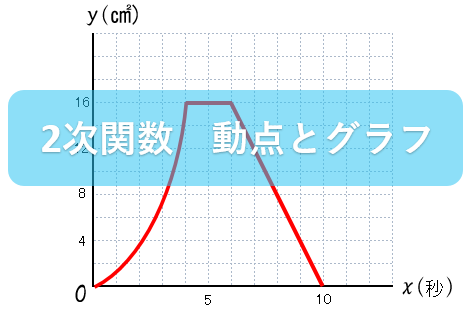



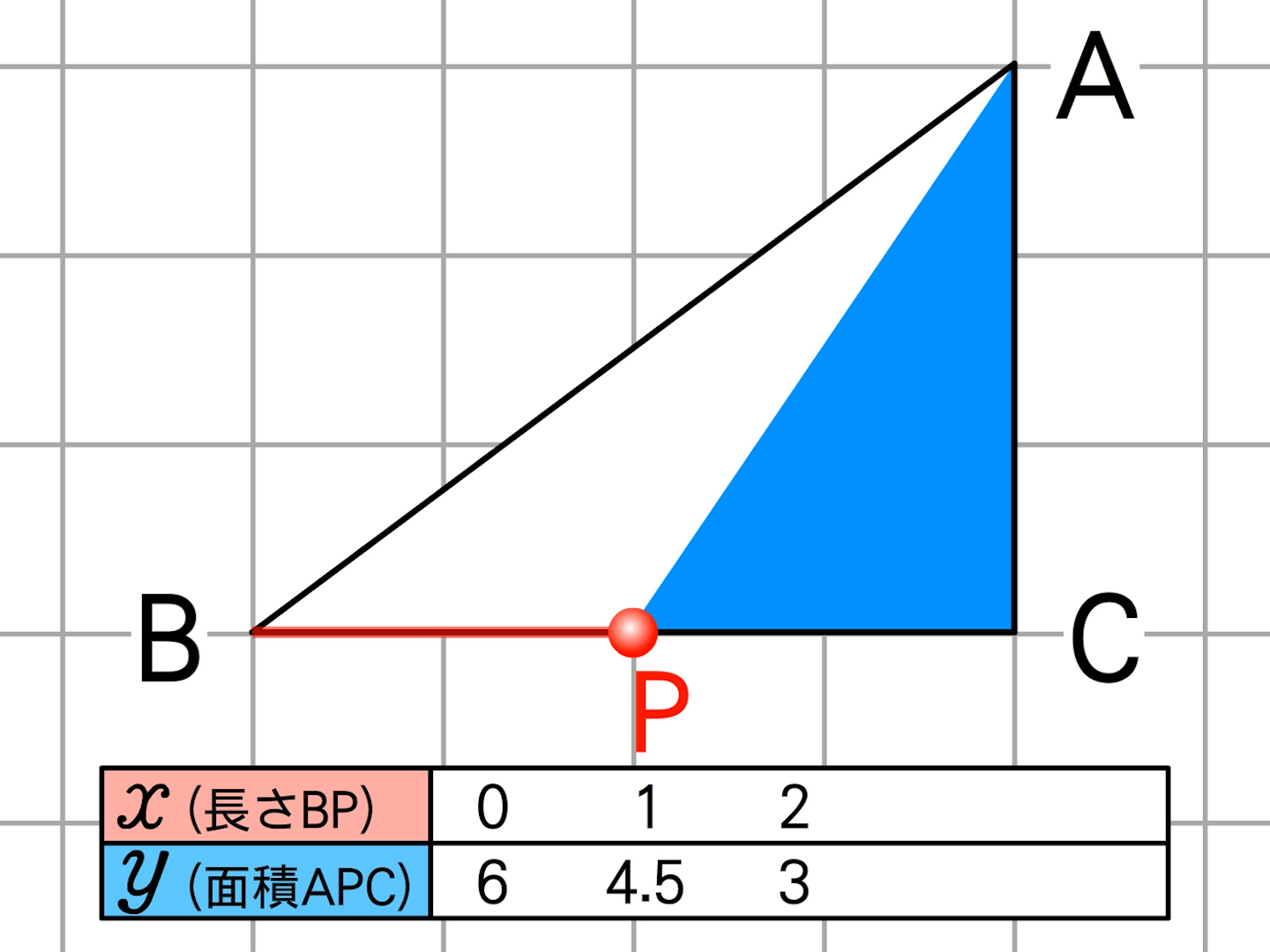
中3数学 2次関数指導案 動点とグラフの問題について丁寧な解説がたくさんある授業




標準 四次関数と微分 なかけんの数学ノート
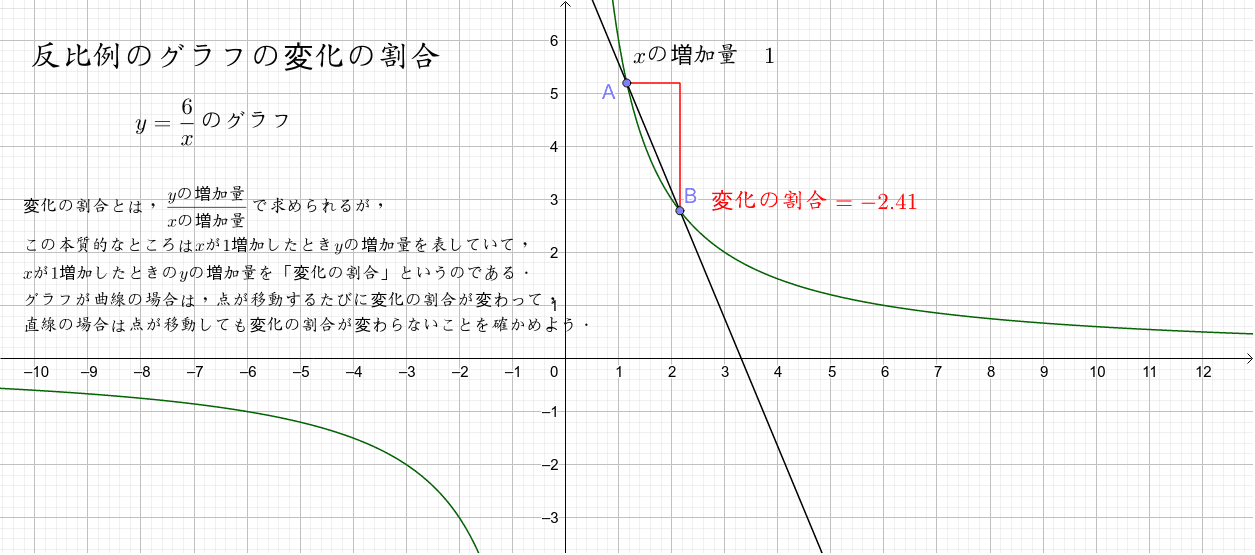



1次関数 反比例 2次関数の変化の割合 Geogebra




2次関数の平方根の関数 代用品の話 Accademia Nuts
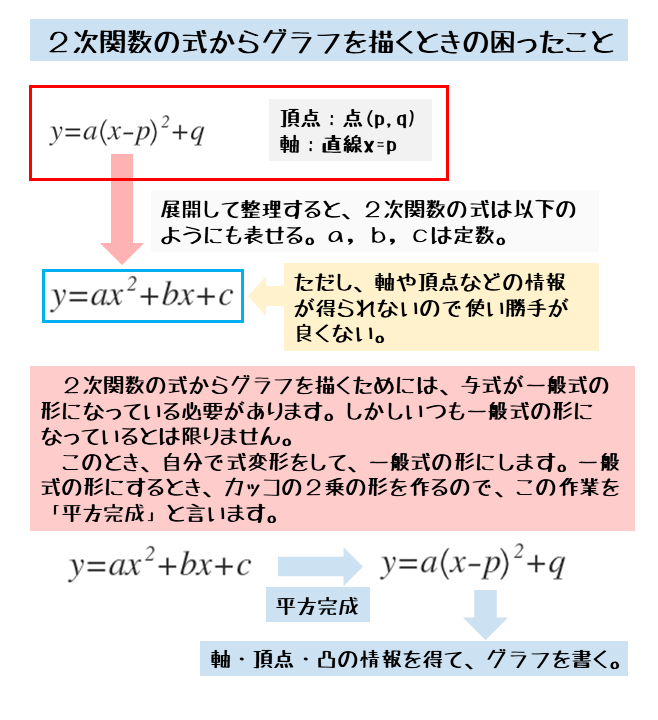



2次関数 2次関数の平方完成について 日々是鍛錬 ひびこれたんれん



中学数学 1次関数 グラフの読み取り 中学数学の無料オンライン学習サイトchu Su
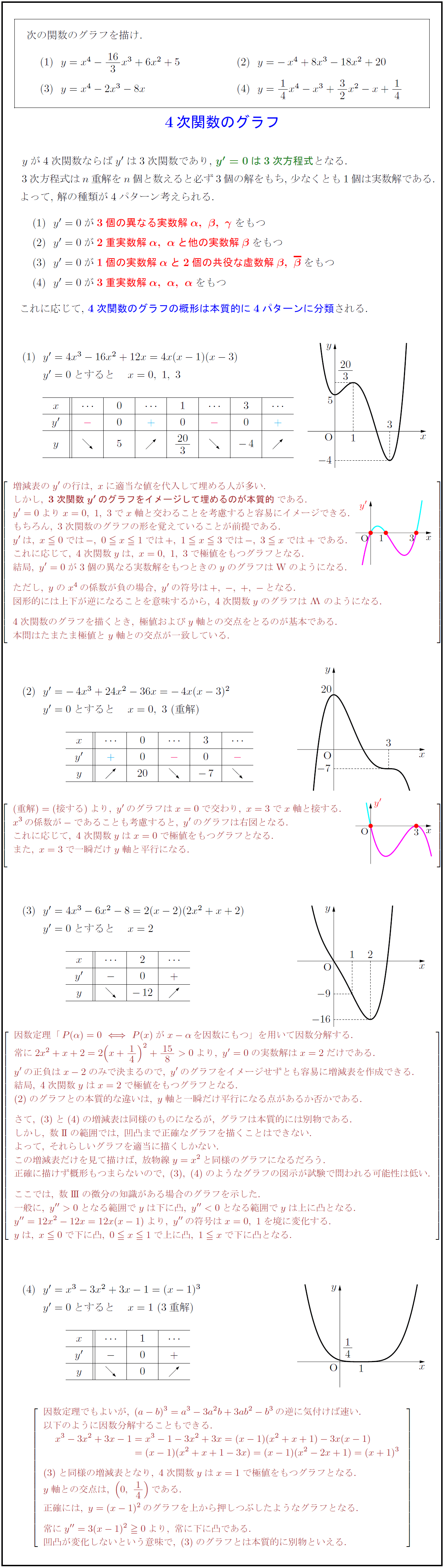



高校数学 4次関数のグラフの図示 受験の月




関数は 答えが出てくる便利な箱 と理解する 中高数学おさらい 1次 2次関数 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン




中学入試の問題 5 9 13 21 に入る数はなに 金 重明 ブルーバックス 講談社 3 4
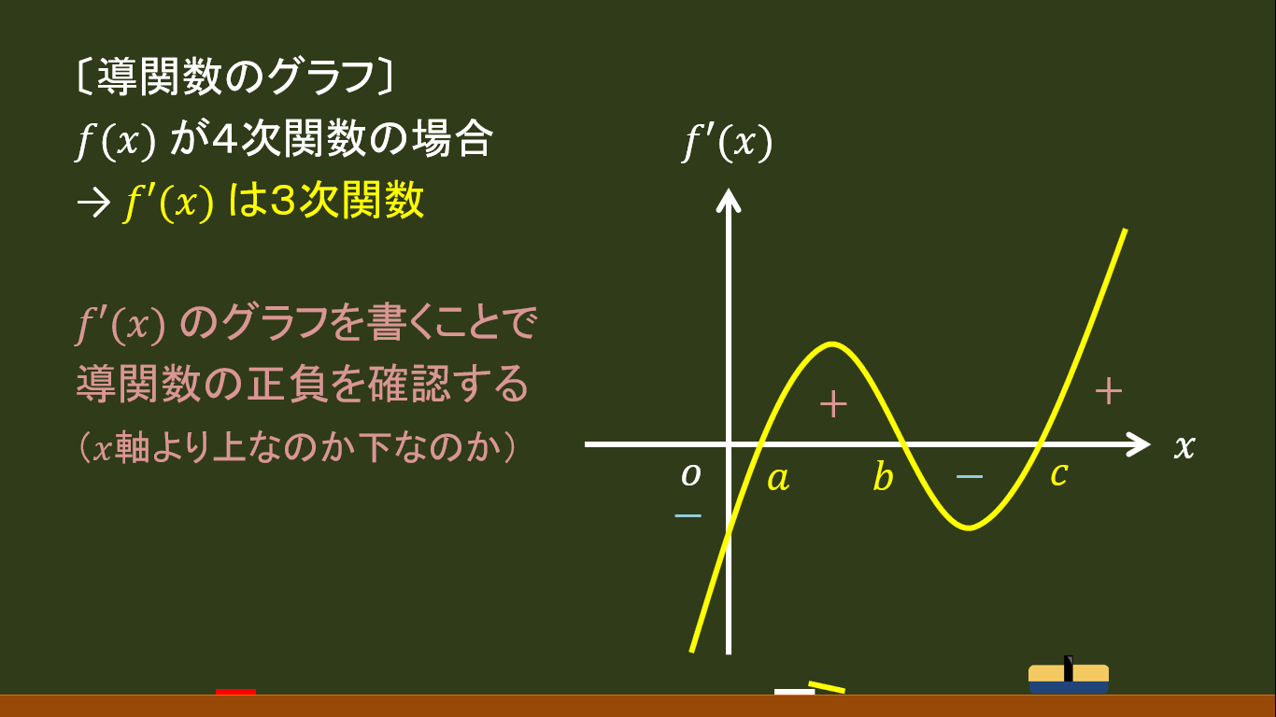



質問 数学 F X が4次関数の場合の増減表 オンライン無料塾 ターンナップ




2次関数 P と Q が放物線の頂点 高校数学2次関数の式の完成の巻 Vol 10 Kazアカデミー 大阪の看護学校 看護予備校
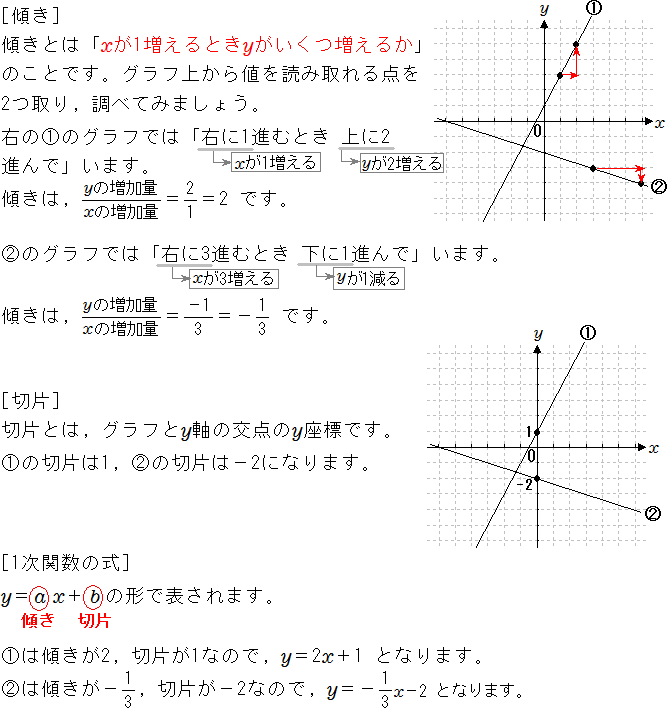



1次関数 1次関数のグラフの読み取りの基礎 中学数学 定期テスト対策サイト




2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ



零次関数 Neutral Ownd




4次関数の2重接線の方程式と囲まれた部分の面積 数学の偏差値を上げて合格を目指す



2




数 2次関数 関数の平行移動 操作は簡単 意味は深い 教えたい 人のための 数学講座
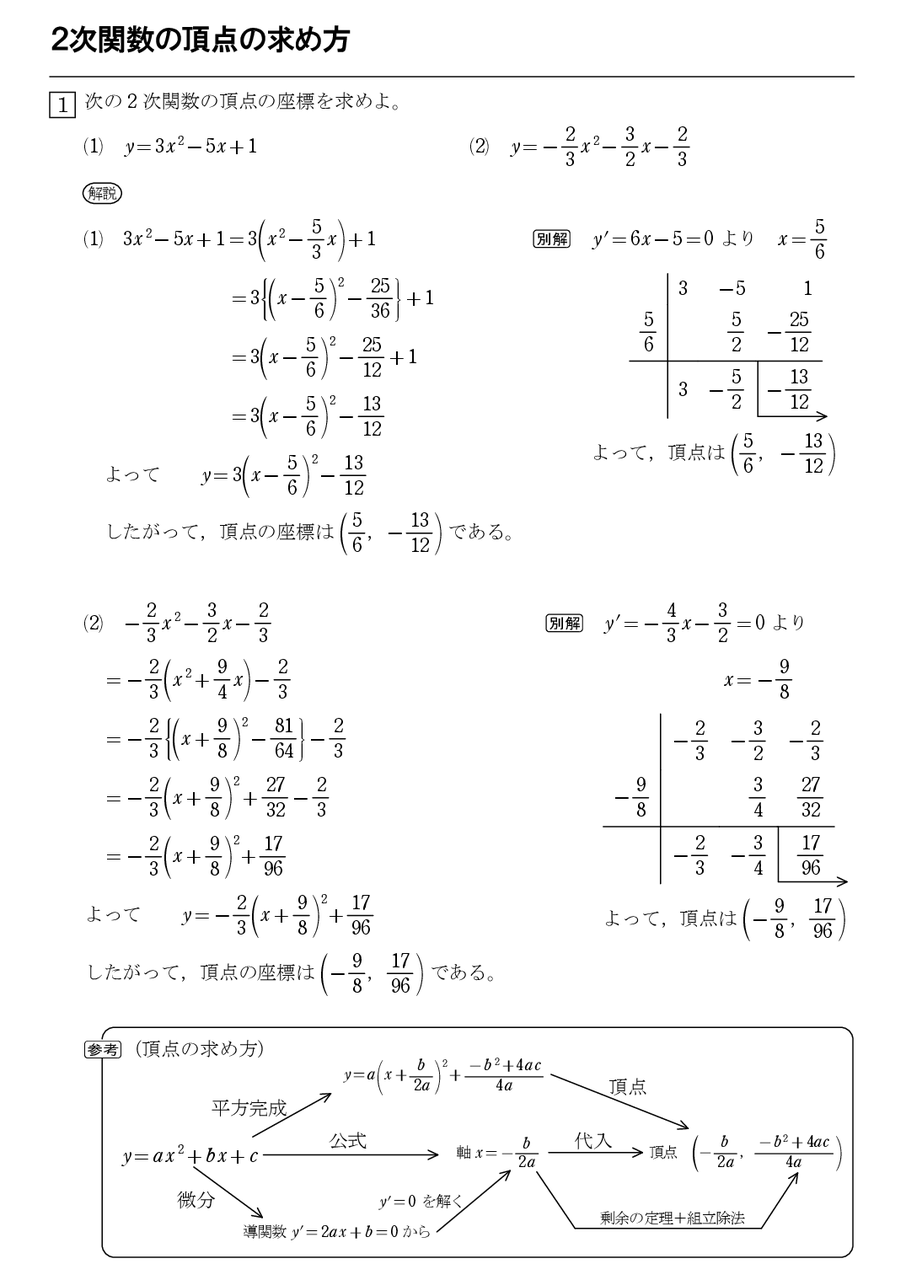



2次関数の頂点を求める別解 怜悧玲瓏 高校数学を天空から俯瞰する
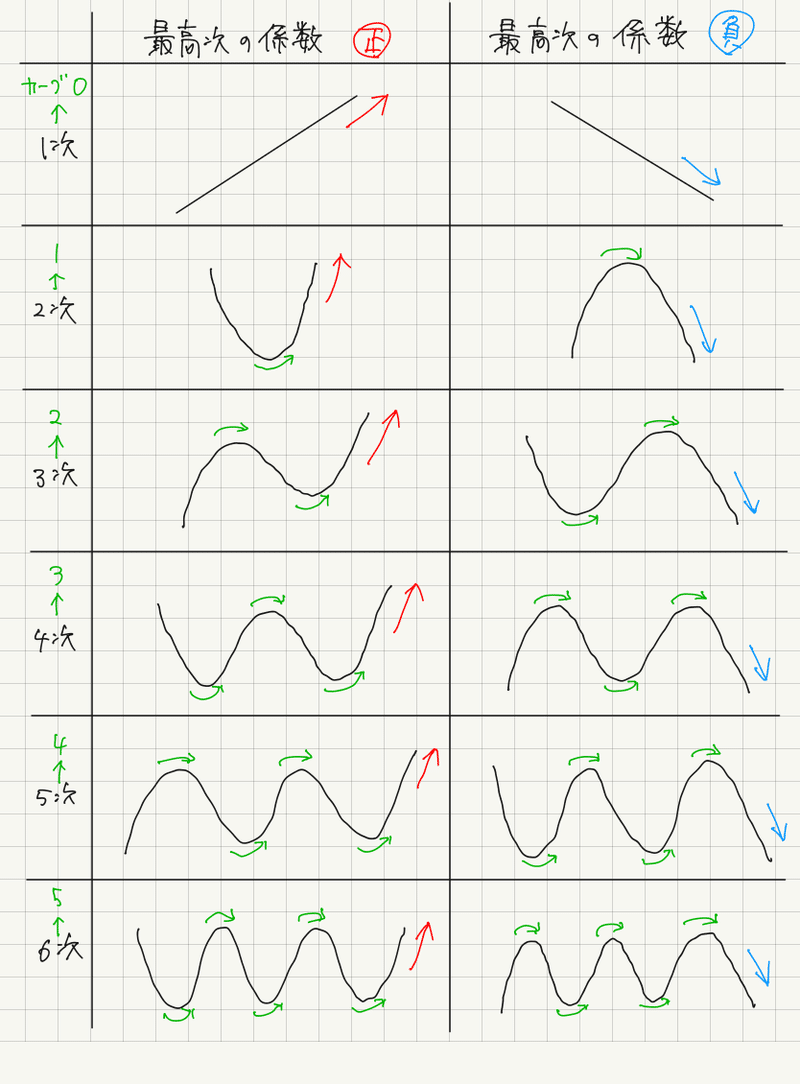



N次関数のグラフの概形 関谷 翔 Note



1次関数のグラフとは 5分でわかる描き方 特徴 式 傾き 分数との関係




高校数学 数 49 2次関数の決定 Youtube




中学3年生 数学 2次関数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
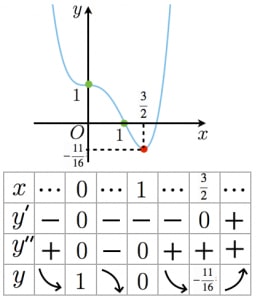



四次関数の二重接線を素早く求める方法 高校数学の美しい物語



2




1次関数の式と座標 計算ドリル 問題集 数学fun
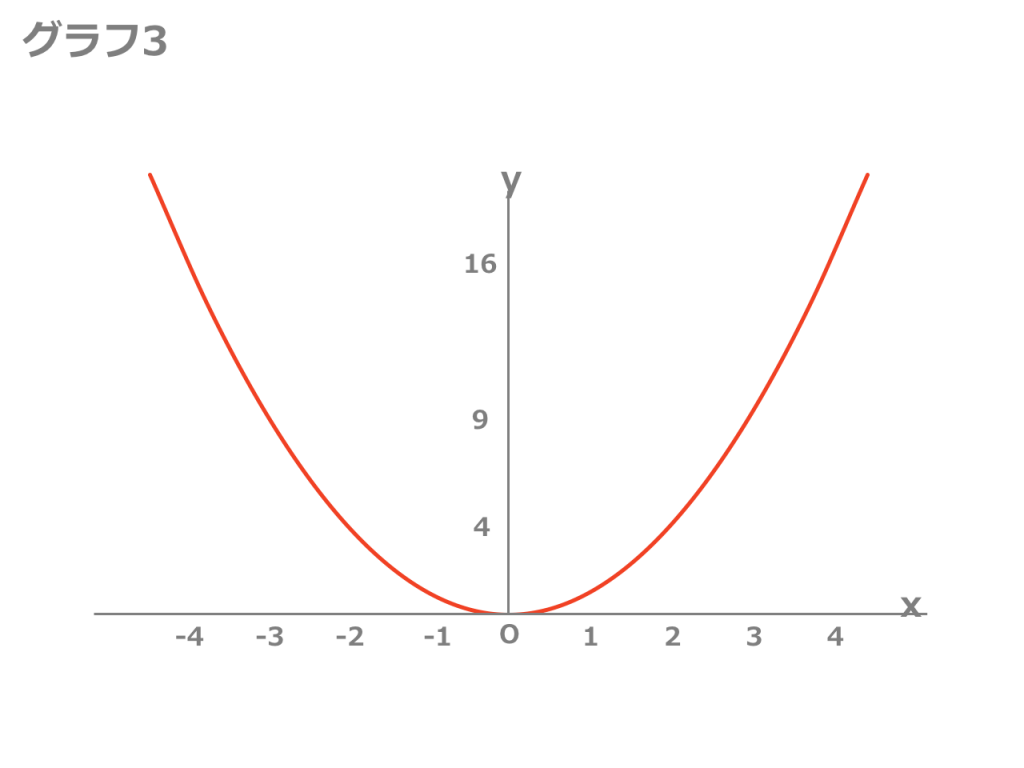



3分で分かる 2次関数のグラフの描き方をわかりやすく 合格サプリ




中学2年生 数学 1次関数の活用 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




2次方程式から2次関数を考える 数学i フリー教材開発コミュニティ Ftext




数学1 2次関数勉強法 センター数学頻出の2次関数をマスターするポイント
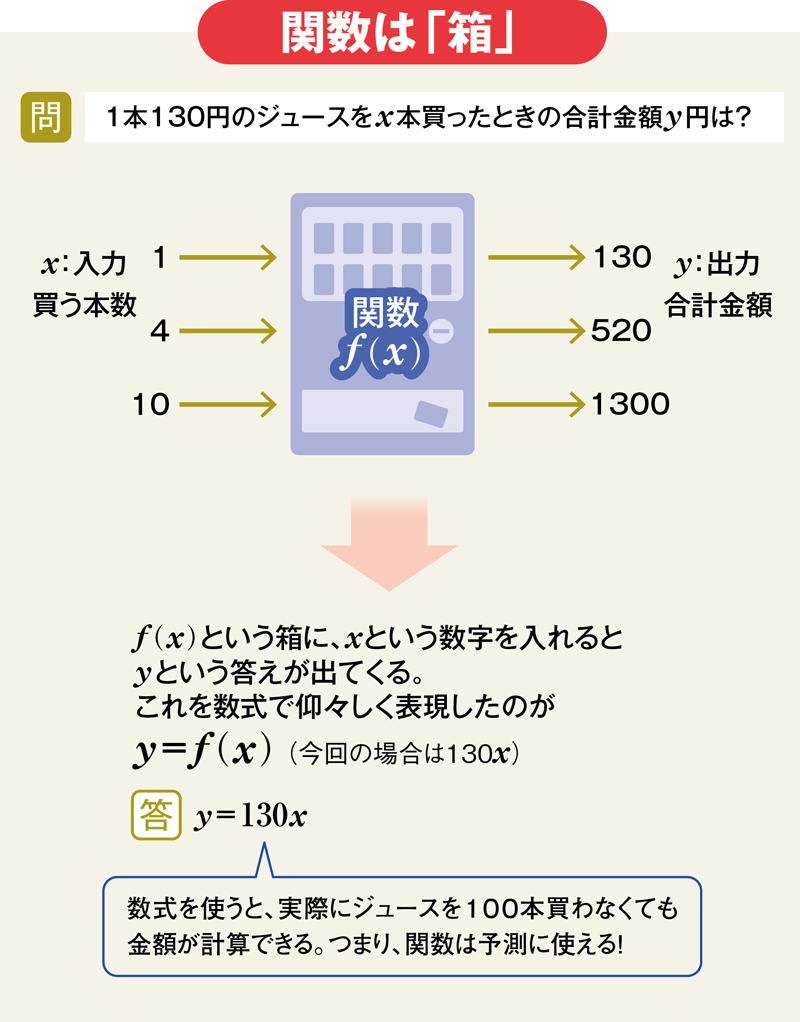



関数は 答えが出てくる便利な箱 と理解する 中高数学おさらい 1次 2次関数 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン
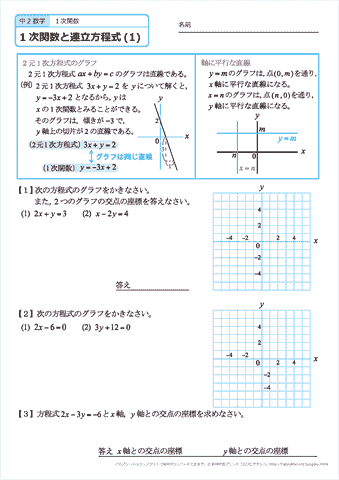



中学2年生 数学 1次関数と連立方程式 文章題 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




場合分けのやり方について 数学 苦手解決q A 進研ゼミ高校講座




数 2次関数 標準形の求め方 素早く頂点を求める手法の紹介 教えたい 人のための 数学講座
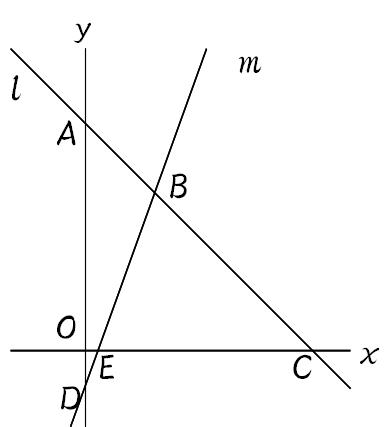



Mathematics 1次関数 6 応用問題の解き方 1 1次関数と図形 働きアリ



整数点を4つ通る3次関数式について 用 高精度計算サイト



1次関数のグラフ3



二次関数の移動



3次関数のグラフと接線



2次関数の各係数の意味
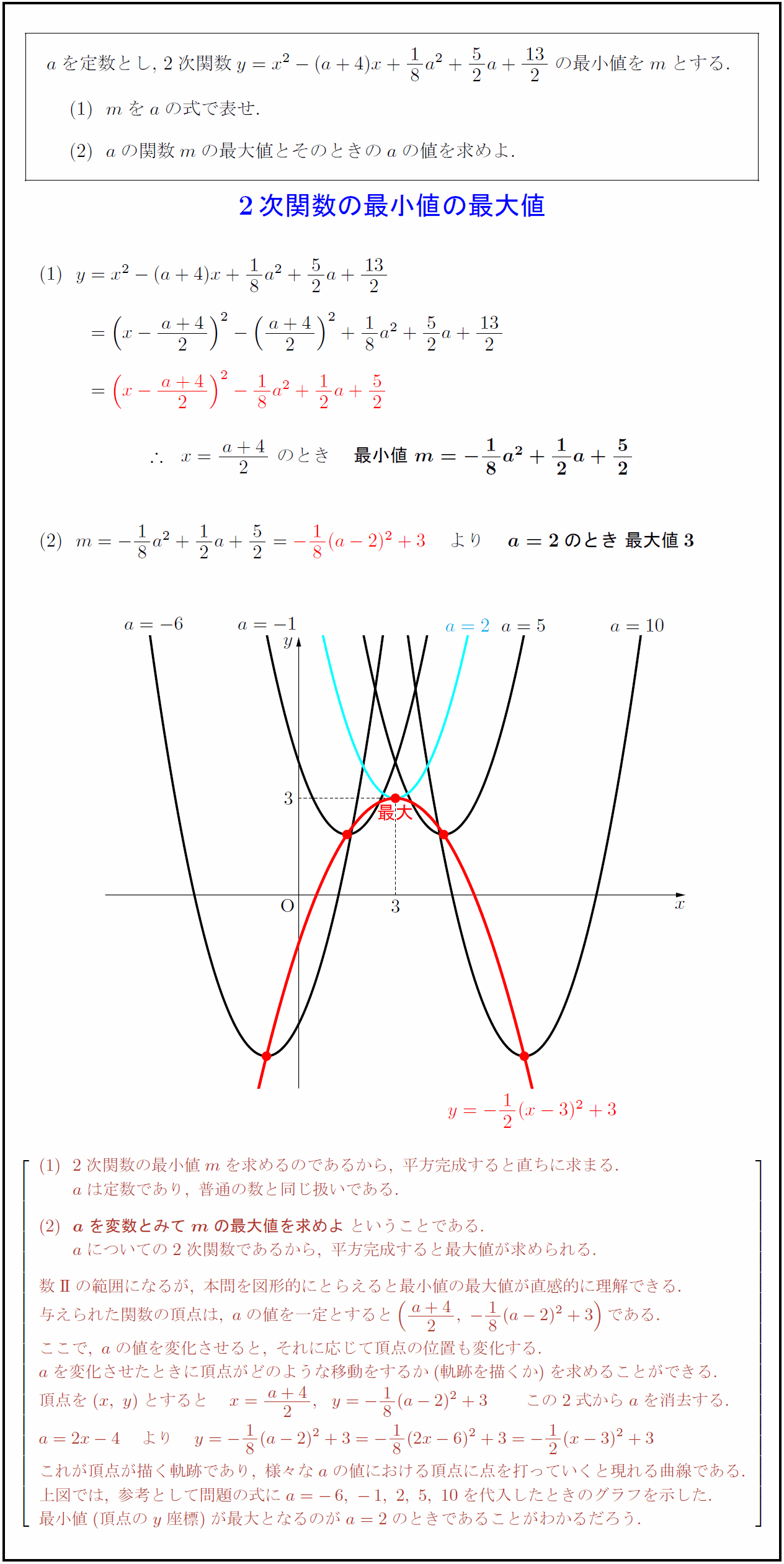



高校数学 文字を含む2次関数の最小値の最大値 受験の月




数 2次関数 関数の決定その1 頂点と軸が分かる場合 平行移動と媒介変数がポイント 教えたい 人のための 数学講座



数学i 基礎 解説 例題コース 2次関数 実用 石井大裕 電子書籍試し読み無料 Book Walker
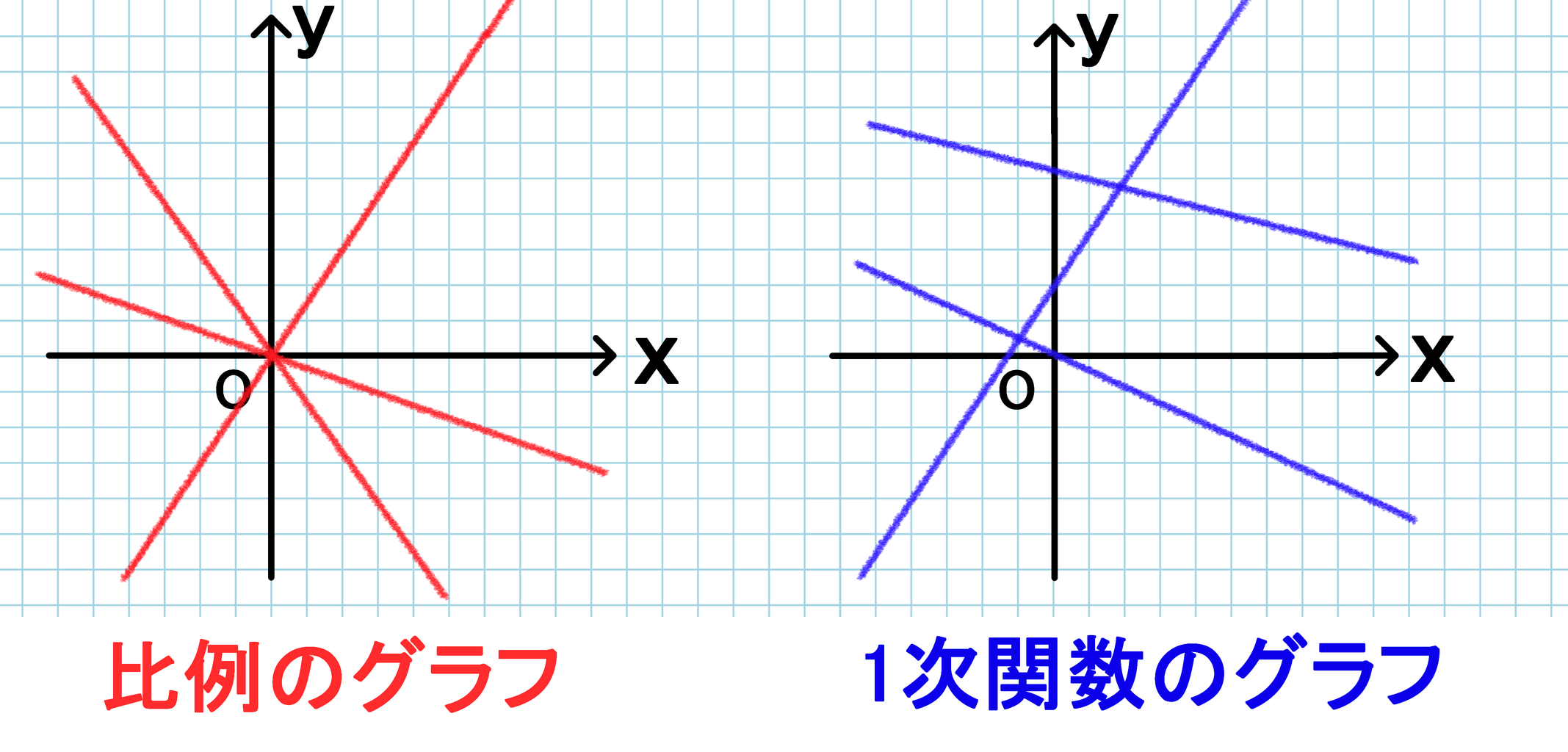



1次関数と比例の違いとは バカでもわかる 中学数学



0 件のコメント:
コメントを投稿