単元 比例式, 「中学1年生で勉強する 数学の1次方程式の説明を 分かりやすくしていきます。」, キーワード 中1数学,1次方程式,基本,要点,小数整数,分母,最小公倍数,解き方,勉強法,復習,勉強方Pocket 今回の記事では、中1で学習する一次方程式の解き方についてまとめていくよ! 基本的な方程式の解き方から分数、小数を含む方程式の解き方まで説明していきます。 分数、小数が出てくると難しく思えちゃうんだけど、ある手順をしっかりと踏めば 方程式の解き方 (例1)x+3=6を解きましょう。 この例で、移項のルールを確認します。 x+3=6ー3 今回、「+3」という項を移項するので、移項す るときに+をーに入れ替えます。 やっていることは基本と変わりませんが、ひと手 間抜いて、瞬時に引いてしまいます。 大人塾 8

中学1年数学 一次方程式 一次方程式の解き方 移項の本当の意味を理解すれば全部解ける 数学の面白いこと 役に立つことをまとめたサイト
方程式の解き方 中1
方程式の解き方 中1-Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed out Videos you watch may be added to the TV's watch history and influence TV中2 数学1次関数の問題(1)問題と解説 方程式の解き方・等式の性質問題と解き方 中学2年生の数学1次関数の基本問題プリント問題と解説 まだ間違った勉強法で苦労し続けますか




一次方程式の解 計算ドリル 問題集 数学fun
正解は「1」です。 ここで中学生らしく、 をxに代えて書き直すと、 x+2=3 (1) x=1 となります。 文字を使って書くと難しそうに見えますが、 を使っていたのをxに置き換えただけなので、あまり身構えないでください。 (1)式のように、不明な文字を含む等式(=で結ばれた式)を「方程式」といい、その文字の値をもとめることを「方程式を解く」といいます 中1数学にでてくる1次方程式(xの方程式)の解き方 こんにちは! イボコロリを使ってみたKenだよ。 中1数学でむずかしいと言われているのは「 方程式 」。 中1で勉強するのは「 1次方程式 」とよばれているものだ。 なにせ、文字が1つしか含まれていないからね。 今日は 「一次方程式」の解き方 の手順を3つにわけて紹介するね。 でも、中1で勉強する1次方程式 方程式については、中1で文字が1つのタイプ、 中2では文字が2つのタイプの方程式を習いましたね。 では中3で習う方程式とはどんな方程式とはでしょうか? 今までの流れで行くと"文字が3つ"となりそうですが、 実は文字は1つに戻ります。 その代わりと2次式が登場します。 ではこの2次方程式、バッチリ理解していきましょう。 1 2次方程式の解き方 2次方程式の
数学が苦手な人向けに動画をUPしています。時間がない方は下のリンクから特定の場所だけでもどうぞ!008 移項の説明101 例題3508 解を与えられ このページは、こんな方へ向けて書いています 一次方程式の解き方を丁寧に説明して欲しい 移項って何?勝手に項を移動させていいのはなぜ? 移項で符号が変わるのはなぜか知りたい ここでは、中学校の1年生で習う一次方程式の解き方を丁寧に解説します。 まず、一次方程式とはどのよう 中学1年生 中1の方程式🐰 方程式の基本 方程式の解き方 移項による解き方 を中心的にまとめてみました🐣 参考にしてくれたら嬉しいです🐯 中1 方程式 このノートが参考になったら、著者をフォローをしませんか?
単元 方程式とその解き方,1次方程式の利用,比例式, 「中1数学で習う数学の単元「方程式」を、トライイットの今川和哉先生の授業を元に まとめました。「方程式」では文字を使うだけではなく文字の値を求められます。 また、方程式を活用した問題も出てくるので、数学に必要な「活用性方程式の解き方2 「両辺に同じ数字をかけても等式は成り立つ」 この性質を利用してxに係数がある方程式を解く。 xに係数があったら、 係数の逆数 をかけて1にする。 例 方程式 –3x = 12 の解き方 xの係数は 3 なので、 両辺に3の逆数をかけて 、両辺 2本(以上)の直線が交わる点 交点の(6,5)は = y = 2 3 x 1 と = y = − x 11 の2つのグラフが どちらも通っていますね 「グラフが通る点= x と y が方程式の解になる」 となり 2つの方程式の解→連立方程式の解




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



無料 中1数学 基本解説 問題プリント 方程式2 解き方1 123
③過不足の問題にチャレンジ! 方程式の利用の中でも、「 過不足の問題 」は解くためのコツが必要になります。 次の「過不足の問題」を使って、解き方を説明していきたいと思います。 「何本かの鉛筆があります。子どもに1人5本ずつ配ると、3本あまります。復習連立方程式の解き方 連立方程式とは、一般的に \begin{eqnarray}\left\{\begin{array}{l}axby=c\\dxey=f\end{array}\right\end{eqnarray} といった形で表すことが多い式です。 2元1次方程式と呼ばれる「2つの変数(文字)」と「最大次数が1」の式で表されます。 連立方程式の解き方は大きく2つあります。それは、== 連立1次方程式の解き方(まとめ) == 連立1次方程式とは,次の形の方程式をいい,一般に未知数をn個含む1次方程式から成り立っている.このページでは未知数が2個~4個の場合を扱う.



中3 二次方程式の基本解説 中学数学の方程式 中間 期末テスト 高校入試対策




中学数学 一次方程式
Check 中1・数学方程式の解き方を基礎から解説! 授業動画あり 中1・数学方程式の解き方を基礎から解説! 授業動画あり 今回は「一次方程式」の解き方についてみていきましょう。 文字がたくさん出てきたりと慣れない計算に苦戦している人も多いのではないでしょうか? 解き方をしっかり理解すればどんな方程式もスラスラ解けるようになり 簡単に解くための、たった2つポイントとは中1 方程式 中学数学 数学 数学おじさん 今回は、一次方程式の解き方のコツをお話ししようと思うんじゃ 一次方程式の解き方として、教科書に書いてあるのは、 等式の性質 移項(いこう) といった内容になるわけじゃ これらは、方程式を解くときの、公式のようなものじゃな これらは、数学をきちんと理解する一次方程式はイコールのバランスさえ取れていれば、両辺にをかけたって、100をかけたっていいわけですから。 一次方程式の分数の問題の解き方。 それは「分母じゃま!」と考えることから始めればよいと思います。 スポンサーリンク




中1 数学 一次方程式 中学生 数学のノート Clear




中2数学 連立方程式の解き方と定期テスト予想問題 Pikuu
方程式とはなにか?方程式の解とは?移項とは? 方程式の項目で必要な用語と名前から説明しますので何も知らなくて大丈夫です。 ここでは中学1年の数学で解いていく1次方程式の解き方を基本的な問題の中で解説します。 方程式が出て動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru 中1方程式って何? 解き方まで分かりやすく解説 中2連立方程式「食塩水の濃さ」の考え方・解き方 中1文字と式 数量の関係を等号・不等号



無料 中1数学 基本問題 解答プリント 方程式2 解き方1 123




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
中1数学「方程式」がわからない人は、以下の順でTry ITの映像授業を観て勉強してみてください。 「方程式の解き方」に関する6のポイントを覚える 「方程式の利用」に関する3のポイントを覚える 「比例式」に関する1のポイントを覚える まずはこれらのポイントをしっかり覚えてから、練習や例題にある問題を解いて「方程式」のわからないを克服しよう。動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru方程式 要点 方程式の解き方 中1数学の方程式の計算問題を徹底的に練習 中学校数学学習サイト トップページ サイトマップ 更新履歴 サイトについて お問い合わせ 解説リクエスト 数学の要点 練習問題 解説 pcスマホ問題 例題 学習アプリ 高校数学学習サイト 中学学習サイト 中学理科の




中1方程式 かっこがあるときの解き方を問題解説 Youtube
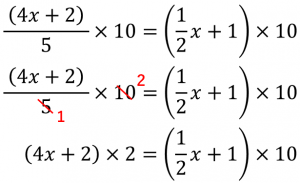



中1数学 方程式 分数をふくむ方程式ってどう解くの たけのこ塾 勉強が苦手な中学生のやる気をのばす
方程式の解き方は、 x= の形 にすることだったよね。 これまでの解き方では、ジャマな+1を消すために、左側と右側、両方に-1をしたよね。方程式の解き方は、 x= の形 にすることだったよね。 今回、x= の形にするためにジャマなのものはどれだろう。 そう、2xの、「2」の部分だね。 2xに1/2をかけてやろう 。方程式 要点 方程式の解き方 中1数学の方程式の計算問題を徹底的に練習 中学校数学学習サイト トップページ サイトマップ 更新履歴 サイトについて お問い合わせ 解説リクエスト 数学の要点 練習問題 解説 pcスマホ問題 例題 学習アプリ 高校数学学習サイト 中学学習サイト 中学理科の




中1 数学 中1 33 方程式の利用 お金編 Youtube




中2 数学 連立方程式の解き方二通りを解説 授業動画あり アオイのホームルーム
なお、方程式の解き方については以下の記事を確認して下さい。 中1数学方程式の解き方 ―その1 今回の中1数学の解説は方程式の解き方について解説していきます。 まずは方程式とは何か、どのようにして解くのかを解説していきます。 解き方に 小・中必見ー1次方程式の考え方ー 21年2月1日 移項などをややこしく感じている人のための方程式の解き方 です。 さくらっこくん、 4=9 という問題に見覚えはあるかい? 小学校のときにやったよ! に入るのは、 94 で 5 だね。 星野先生 その通り。 それでは、 3× =24 中1数学「方程式とその解」の問題 どこよりも簡単な解き方・求め方 数学では分からない数量を文字(等)で置いて等式を作り、その等式を使って数量を求めることができます この「まだ分かっていない数量を表す文字を含む式」のことを「方程式」と言います この方程式の「等式の




一次方程式の解き方 いろいろな計算練習 無料で使える中学学習プリント




中学1年生 数学 無料問題集 一次方程式 おかわりドリル



無料 中1数学 標準問題 解答プリント 124 方程式3 解き方2




中1 数学 方程式 中学生 数学のノート Clear




中学1年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




例題付き 連立方程式の解き方と失敗しないコツ




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




一次方程式の解 計算ドリル 問題集 数学fun
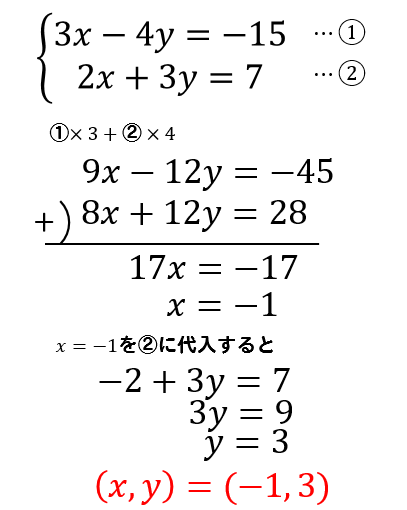



連立方程式 加減法の解き方をわかりやすく問題を使って徹底解説 数スタ




誰でもわかる数学 中学3年 2次方程式の解き方 Youtube



中3 二次方程式の解き方 平方根 因数分解 中学数学の方程式 中間 期末テスト 高校入試対策
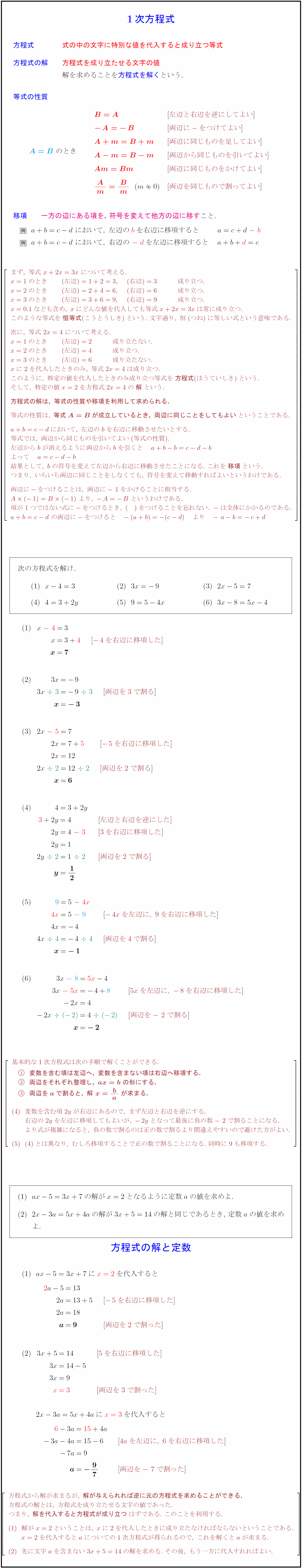



中学数学1年 基本的な1次方程式 方程式の解と定数 受験の月




高校数学で学習する連立方程式の解き方まとめ 数スタ



中1 一次方程式のかっこは外してから解こう 中学数学の方程式 中間 期末テスト 高校入試対策




方程式の解き方 簡単な問題で 解き方のコツを覚えよう 中学や高校の数学の計算問題
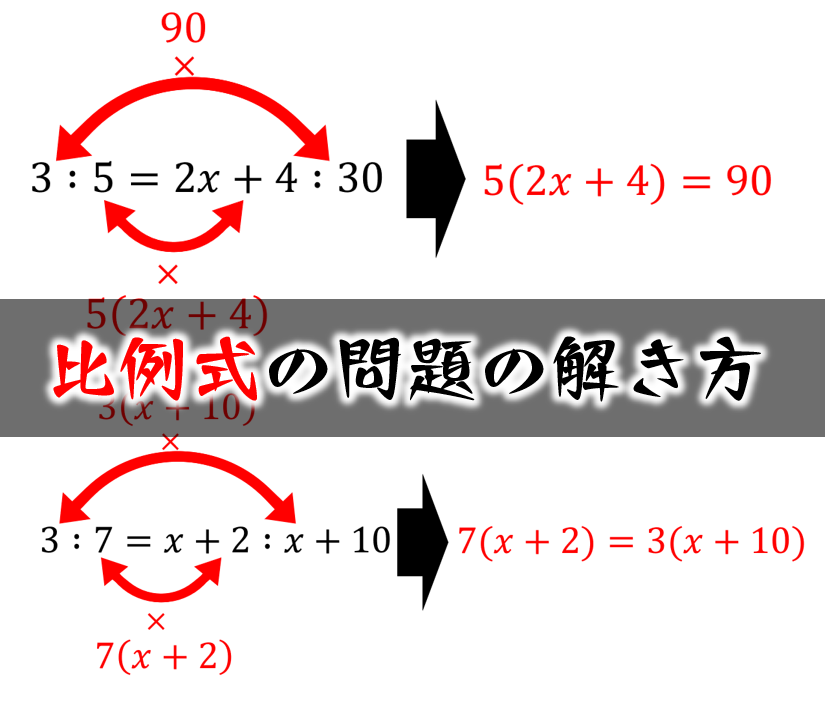



比例式の問題の解き方 数学fun




中学数学1年 1次方程式の利用 整数 受験の月




方程式の種類と解き方 中学で学習する方程式ってどんなのがある 中学数学 理科の学習まとめサイト




分数の方程式の解き方 分母を消せば中1の子でも絶対解ける 中学や高校の数学の計算問題



無料 中1数学 基本問題 解答プリント 方程式3 解き方2 124




数学 中3 26 二次方程式 解の公式編 Youtube
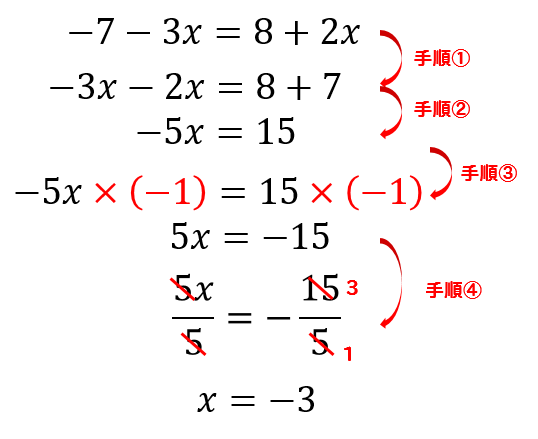



中1方程式 一次方程式の解き方をまとめておくよ 基本計算 分数 小数まで 数スタ




中学1年の数学 動画 方程式を解く 基本編の問題 19ch




二次方程式とは 見分け方が簡単にわかる中学レベルの問題 中学や高校の数学の計算問題




中1 数学 方程式の解き方を基礎から解説 授業動画あり アオイのホームルーム




1次方程式の解き方 1 無料で使える中学学習プリント




中学1年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中1 一次方程式を 移項 で解く 中学数学の方程式 中間 期末テスト 高校入試対策




中1数学 方程式 2 3 かっこを含む1次方程式 Youtube




中1 1次方程式 でつまずく原因と解決法 分数




分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題




方程式の利用 一次方程式の文章題の4つの解き方 Qikeru 学びを楽しくわかりやすく
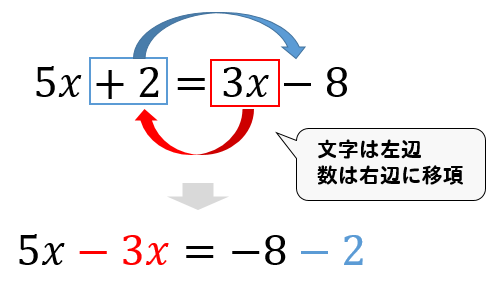



一次方程式の解き方を解説 かっこや分数の場合のやり方も 方程式の解き方まとめサイト



U9j580gf8iba369ji2w Xyz P 703



無料 中1数学 基本解説 解答プリント 方程式3 解き方2 124
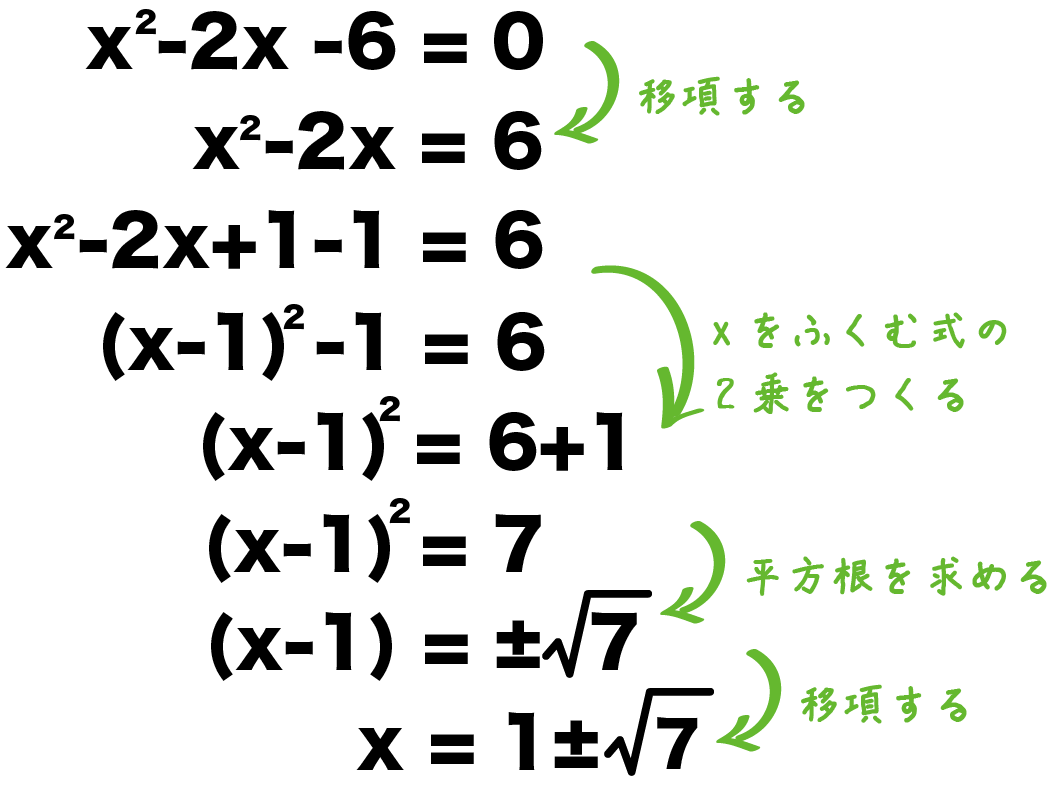



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく




中1 数学 中1 29 方程式の解き方 編 Youtube




中1数学 方程式の解き方1 移項 映像授業のtry It トライイット



1



1




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学1年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1方程式 分数が含まれるときの解き方を問題解説 Youtube




中1 いろいろな一次方程式 中学生 数学のノート Clear
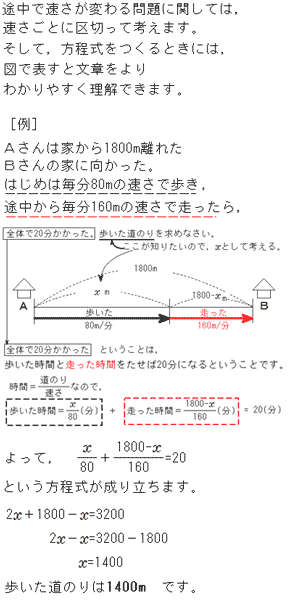



方程式 途中で速さが変わる問題の解き方 中学生からの勉強質問 数学 進研ゼミ中学講座




連立方程式の利用の問題の解き方 年齢の問題 1 現役塾講師のわかりやすい中学数学の解き方




中1数学 比例式の解き方 映像授業のtry It トライイット




数学 中3 24 二次方程式 基本編 Youtube




中1 数学 中1 30 方程式を解く 小数と分数編 Youtube
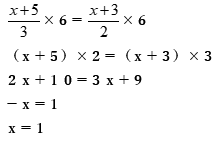



方程式の解き方をマスターしよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導




徹底解説 連立方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



1




中学1年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



中3 二次方程式の解き方 解の公式 中学数学の方程式 中間 期末テスト 高校入試対策




一次方程式の解の求め方 数学fun




二次方程式の解き方のまとめ 中学生に覚えてほしいパターンは5つ 中学や高校の数学の計算問題




中1数学 5分でわかるシリーズ いろいろな方程式の解き方 ふるやまんのマスラボ奮闘記




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




中1数学 分数を含む方程式の解き方 Youtube




中学1年数学 一次方程式 一次方程式の解き方 移項の本当の意味を理解すれば全部解ける 数学の面白いこと 役に立つことをまとめたサイト




中1 数学 方程式5 解き方のコツ 10分 Youtube




中学2年数学 連立方程式 加減法を使った連立方程式の解き方 実際に問題を解きながら解説 数学の面白いこと 役に立つことをまとめたサイト




中1 数学 中1 28 方程式の解き方 基本編 Youtube




中1数学 方程式 14h 中学数学高校数学個別指導in山形市 数専ゼミ
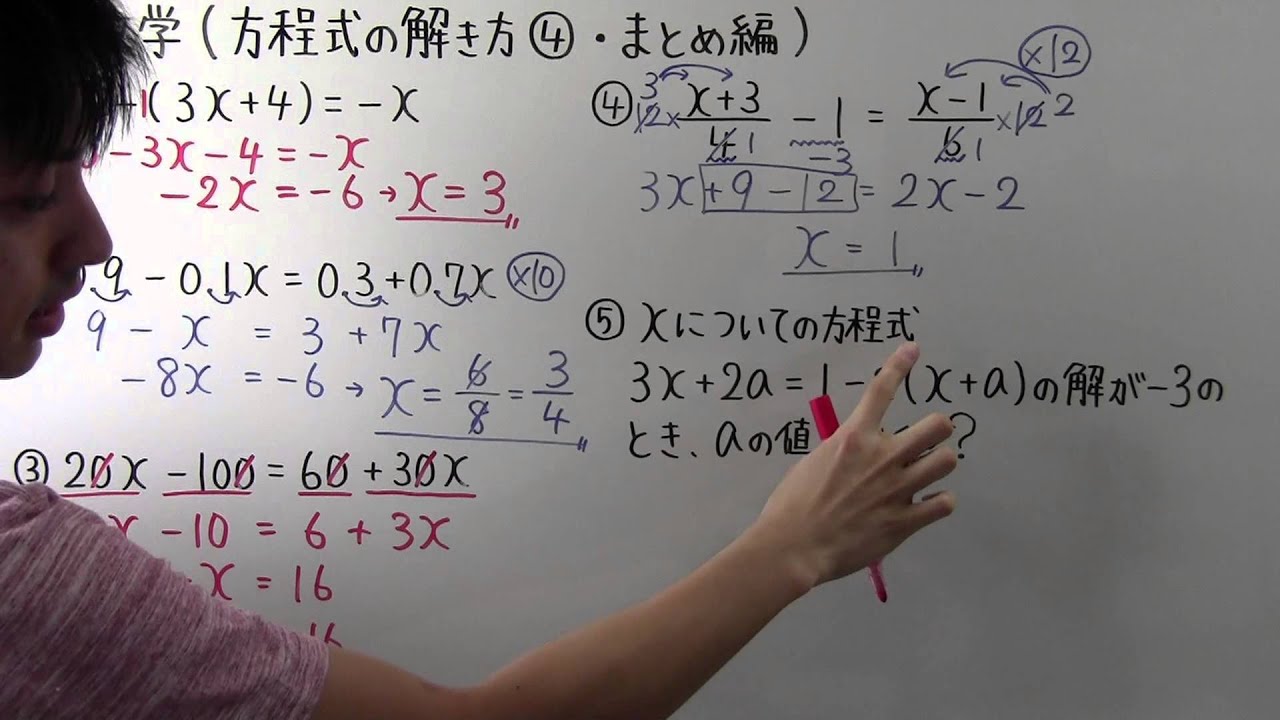



中1 数学 中1 31 方程式を解く まとめ編 Youtube
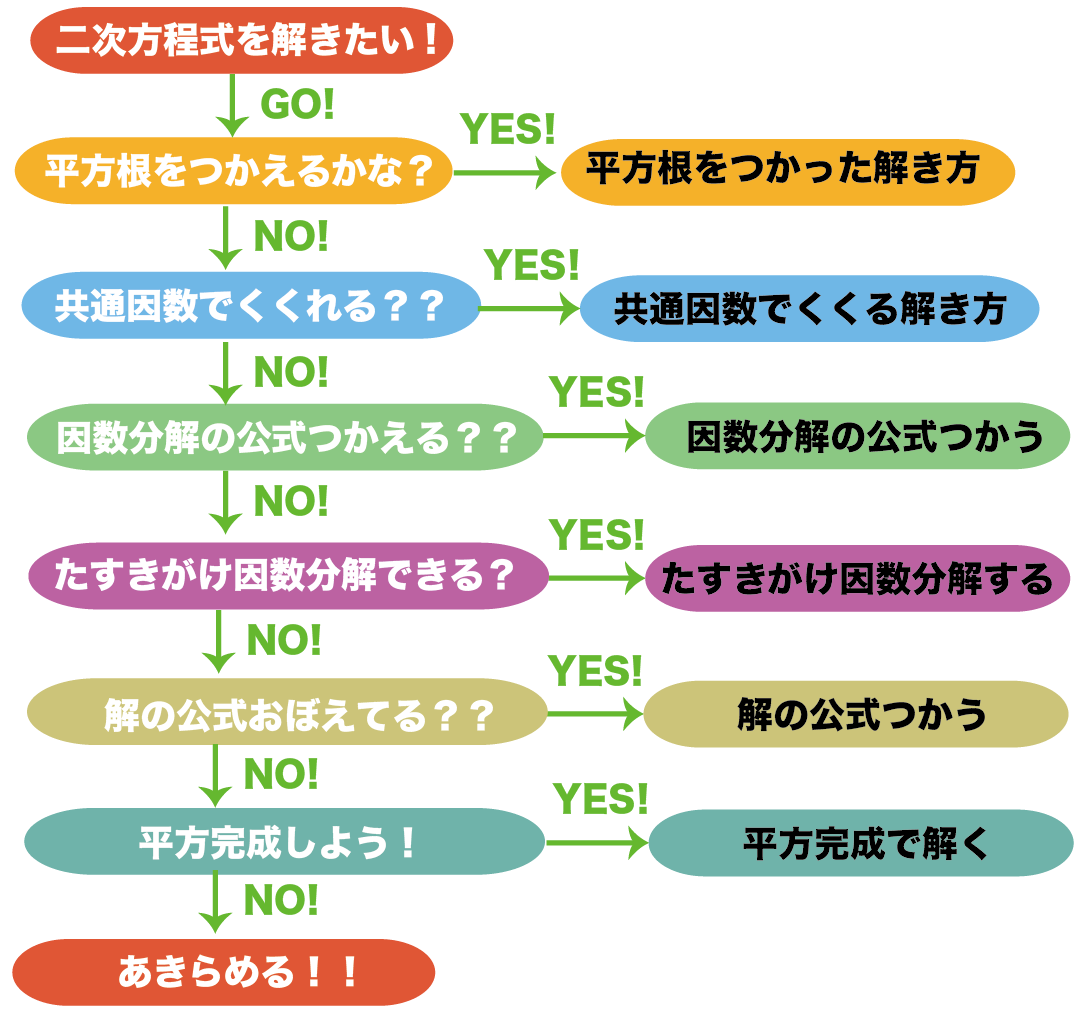



中3数学 二次方程式の解き方を見分ける1つのコツ Qikeru 学びを楽しくわかりやすく
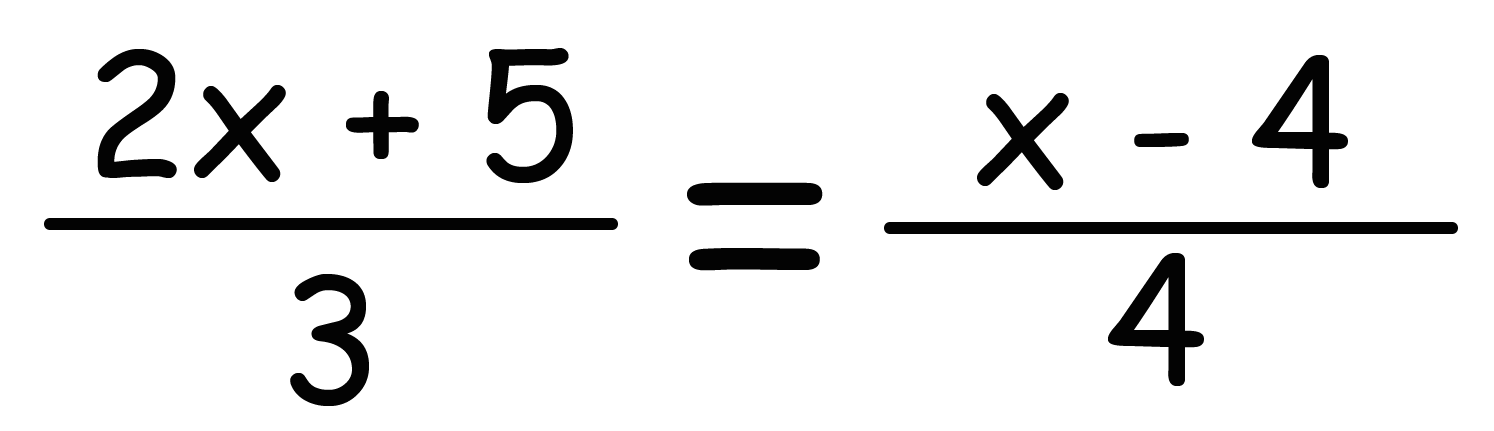



中1数学 分数をふくむ方程式の解き方 Qikeru 学びを楽しくわかりやすく




数学 方程式の解き方をわかりやすくまとめました 簡単に解くための たった2つポイントとは 中1 方程式 中学数学 数学 行間 ぎょうのあいだ 先生



無料 中1数学 発展問題 解答プリント 方程式3 解き方2




世界一わかりやすい数学問題集中1 3章 方程式




中学1年生 数学 方程式の解き方 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中1 1次方程式の利用 中学生 数学のノート Clear



中1数学 発展 応用問題プリント 方程式の解き方 124




中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点




中1 1次方程式 でつまずく原因と解決法 導入




連立方程式の解き方 Youtube




中1数学 方程式の文章題 速さ 例題編 映像授業のtry It トライイット




中学数学 二次方程式の解き方はこの3パターンだけでok 平方根 因数分解 解の公式 楽スタ
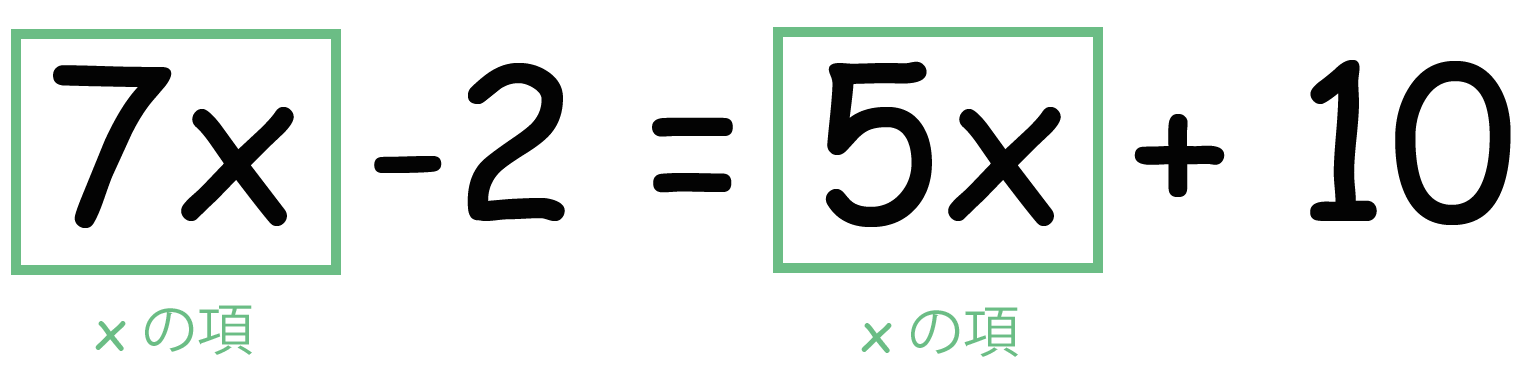



中学数学 1次方程式 Xの方程式 の解き方の3つの手順 基礎編 Qikeru 学びを楽しくわかりやすく




中3 中3数学 2次方程式 中学生 数学のノート Clear




連立2元1次方程式を自由に解こう 中学2年生の数学 身勝手な主張




二次方程式の利用の問題の解き方 整数 3 現役塾講師のわかりやすい中学数学の解き方



2



1




無料 中3数学 基本解説 解答プリント 315 2次方程式1 解き方1




連立方程式の利用の問題の解き方 代金の問題 1 現役塾講師のわかりやすい中学数学の解き方




中学数学 1次方程式 文章題の解き方 代金 個数




3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




中1数学 方程式の解き方4 カッコ 分数 小数 例題編 映像授業のtry It トライイット




数学 中2 14 連立方程式 準備編 Youtube




中1 1次方程式 でつまずく原因と解決法 移項と基本の計算




1次方程式 小数 分数をふくむ1次方程式の解き方 中学数学 定期テスト対策サイト



0 件のコメント:
コメントを投稿